Utilisation scientifique de Python — Deuxième partie : analyse de données

Dans l'article Utilisation scientifique de Python — Première partie : visualisation de données de la Gazette Linux n°114, nous avons fait les premiers pas vers la compréhension et l'interprétation des données scientifiques à l'aide de Python pour les visualiser. L'étape suivante consiste à atteindre une compréhension quantitative en effectuant une analyse pertinente des données, par exemple en ajustant un modèle à celles-ci et en extrayant de ce fait des paramètres utiles. Cette approche constitue le sujet principal de cette seconde partie de l'article Utilisation scientifique de Python. Comme dans la première partie, cet article sera également axé sur des exemples illustratifs. Je pars du principe que le lecteur a lu la première partie de cet article ou qu'il possède des connaissances de base sur Python.

J'ai eu l'agréable surprise de recevoir quelques sympathiques retours de lecteurs sur la première partie de cet article. Certains ont proposé des trucs et astuces additionnels que j'ai ajoutés ici, à l'intention de ceux qui les trouveront utiles, et dont je fais partie.

Si vous voulez essayer tous les exemples sur une machine Windows, John Bollinger suggère d'utiliser os.popen de la manière suivante :

f=os.popen('pgnuplot.exe','w')

Plus intelligemment encore, le code suivant garantit que le script python peut s'exécuter à la fois sous Linux et sous Windows :

import os
import sys

if os.name == 'posix':
    f=os.popen('gnuplot', 'w')
    print 'posix'
elif os.name == 'nt':
    f=os.popen('pgnuplot.exe', 'w')
    print 'windows'
else:
    print 'Systée d'exploitation inconnu'
    sys.exit(1)

JB a également attiré mon attention sur le projet très soigné de Michael Haggerty, gnuplot.py, sur Sourceforge.

Cyril Buttay m'a signalé que l'encodage par défaut dans gnuplot est insuffisant si vous voulez afficher des caractères spéciaux comme les æ, ø et å danois sur les courbes. Pour ce faire, vous devez spécifier un autre encodage, comme décrit dans le manuel de gnuplot :

set encoding {<valeur>}
show encoding

où les valeurs valides sont les suivantes :

default     - demande à un terminal d'utiliser son encodage par défaut
iso_8859_1  - la police Western European la plus couramment utilisée par de
              nombreuses stations de travail Unix et par MS-Windows. Cet encodage est
              connu dans le monde PostScript sous la dénomination 'ISO-Latin1'.
iso_8859_2  - utilisé en Europe centrale et en Europe de l'est
iso_8859_15 - une variante de l'encodage iso_8859_1 qui comprend le symbole de l'Euro
cp850       - codepage pour OS/2
cp852       - codepage pour OS/2
cp437       - codepage pour MS-DOS
koi8r       - encodage cyrillique courant sous Unix

Si vous laissez l'encodage à sa valeur par défaut, les caractères spéciaux peuvent s'afficher sur l'écran mais non sur la copie papier (en fait, je pense que les caractères spéciaux ne fonctionnent que sur le terminal postscript, mais je n'en suis pas sûr). Si le caractère spécial voulu n'est pas disponible sur votre clavier, il est possible d'y accéder par sa valeur octale : par exemple, pour afficher un caractère spécial comme le å danois dans le titre d'un tracé utilisez l'encodage iso_8859_1 :

set title "Ceci est le caractére danois \345"

qui affichera "Ceci est le caractère danois å" dans le titre du tracé. Pour pouvoir transcrire les caractères grecs, comme par exemple α (alpha minuscule), on devra utiliser {/Symbol a} (ce qui nécessite le terminal postscript enhanced). De la même manière, on obtient le Γ (gamma majuscule) à l'aide de {/Symbol G}. Pour trouver les caractères spéciaux et leurs valeurs octales correspondantes pour, par exemple, l'encodage iso8859-1 sous Linux, il suffit de saisir :

man iso_8859-1

ou de jeter un coup d'œil à ce fichier postscript (en anglais).

Le premier exemple illustre comment ajuster un modèle à des données en 2D. Les données à ajuster se trouvent dans le fichier tgdata.dat et représentent une perte de poids (en pourcentage massique) en fonction du temps. Cette perte de poids est due à la désorption de l'hydrogène à partir du LiAlH₄ (ou lithium aluminium hybride), un candidat potentiel pour le stockage d'hydrogène embarqué dans les futurs véhicules alimentés par pile à combustible (merci à Ben d'avoir mentionné l'énergie de l'hydrogène dans The Linux Launderette n°114). En fait, ces données sont les mêmes que celles de l'exemple n°1 de l'article Utilisation scientifique de Python — Première partie : visualisation de donnés^[1]. Pour certaines raisons, je soupçonne que les données peuvent être décrites par la fonction suivante :

f(t) = A1*(1-exp(-(k1*t)^n1)) + A2*(1-exp(-(k2*t)^n2))

Il existe différentes méthodes mathématiques pour trouver les paramètres permettant d'ajuster au mieux les données, mais la plus courante est probablement l'algorithme de Levenberg-Marquardt dans le cas d'une optimisation non-linéaire au sens des moindres carrés^[2]. Cet algorithme fonctionne en minimisant la somme des carrés (restes au carré) définie pour chaque point par :

(y-f(t))^2

où y est la variable dépendante mesurée et f(t) celle obtenue par calcul. Le paquetage Scipy contient l'algorithme de Levenberg-Marquardt sous la forme de la fonction leastsq.

La routine d'ajustement est dans le fichier kinfit.py.txt et le code Python est affiché ci-dessous. Des numéros de ligne ont été ajoutés pour des raisons de lisibilité^[3].

     0  # -*- encoding:iso-8859-1 -*-
     1  from scipy import *
     2  from scipy.optimize import leastsq
     3  import scipy.io.array_import
     4  from scipy import gplt
     5
     6  def residuals(p, y, x): 
     7          err = y-peval(x,p)
     8          return err
     9
    10  def peval(x, p): 
    11          return p[0]*(1-exp(-(p[2]*x)**p[4])) + p[1]*(1-exp(-(p[3]*(x))**p[5] ))
    12
    13  filename=('tgdata.dat')
    14  data = scipy.io.array_import.read_array(filename)
    15
    16  y = data[:,1]
    17  x = data[:,0]
    18
    19  A1_0=4
    20  A2_0=3
    21  k1_0=0.5
    22  k2_0=0.04
    23  n1_0=2
    24  n2_0=1
    25  pname = (['A1','A2','k1','k2','n1','n2'])
    26  p0 = array([A1_0 , A2_0, k1_0, k2_0,n1_0,n2_0])
    27  plsq = leastsq(residuals, p0, args=(y, x), maxfev=2000)
    28  gplt.plot(x,y,'title "Mesure" with points',x,peval(x,plsq[0]),'title "Identification" with lines lt -1')
    29  gplt.yaxis((0, 7))
    30  gplt.legend('right bottom Left')
    31  gplt.xtitle('Temps (h)')
    32  gplt.ytitle('Hydrogene libéré(%)')
    33  gplt.grid("off")
    34  gplt.output('kinfit.png','png medium transparent size 600,400 enhanced')
    35
    36  print "Paramètres finaux"
    37  for i in range(len(pname)):
    38       print "%s = %.4f " % (pname[i], p0[i])

Pour pouvoir exécuter ce code, téléchargez le fichier kinfit.py.txt, enregistrez-le sous le nom de kinfit.py (ou un autre nom si vous préférez). Téléchargez également le fichier de données tgdata.dat et lancez ce script avec python kinfit.py. En plus de Python, il faut avoir installé SciPy et gnuplot (dont la version 4.0 a servi tout au long de cet article). La sortie du programme est tracée à l'écran comme affiché ci-dessous. Une copie papier est également créée. L'option size du terminal png de gnuplot est un peu compliquée. L'exemple présenté ci-dessus fonctionne lorsque gnuplot a été compilé avec libgd. Si vous avez installé libpng + zlib, au lieu de size, faites appel à picsize. De plus, il ne faut pas séparer par une virgule les valeurs de largeur et de hauteur spécifiées. Comme illustré sur la figure ci-dessous, le modèle proposé s'ajuste très bien aux données.

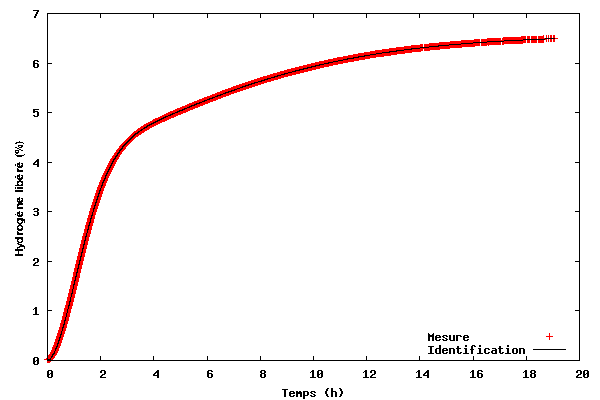
Étudions maintenant le code de l'exemple.

gnuplot utilise également l'algorithme de Levenberg-Marquardt pour sa procédure d'ajustement de courbe. En fait, dans de nombreux cas, lorsque la fonction à ajuster est relativement simple et que les données ne nécessitent pas de prétraitement lourd, je préfère gnuplot à Python — simplement parce que gnuplot affiche l'erreur standard estimée pour chacun des paramètres. Python présente sur gnuplot l'avantage de disposer de nombreux autres algorithmes d'optimisation comme par exemple l'algorithme simplexe, la méthode de Powell, la méthode de Newton ou la méthode du gradient conjugué, etc. Il suffit de fournir une fonction pour calculer la somme des carrés (lorsqu'on utilise leastsq, la mise au carré et la sommation des restes sont effectuées à la volée).

Dans l'exemple suivant, nous allons utiliser la transformée de Fourier rapide (FFT, Fast Fourier Transform)^[4] pour transférer des données chrono-dépendantes dans le domaine fréquentiel. De cette manière, il est possible d'analyser si une fréquence prédominante existe — c'est-à-dire s'il y a une quelconque périodicité dans les données. Nous n'entrerons pas trop dans les détails des mathématiques sous-jacentes à la méthode FFT ; si ce sujet vous intéresse, jetez un coup d'œil à quelques-unes des nombreuses pages informatives que l'on trouve sur l'Internet, par exemple : http://astronomy.swin.edu.au/~pbourke/analysis/dft/, http://www.cmlab.csie.ntu.edu.tw/cml/dsp/training/coding/transform/fft.html, Numerical recipes, etc.

Prenons un exemple simple pour commencer. Intéressons-nous à la mesure de la température à un endroit donné en fonction du temps. Intuitivement, nous pouvons nous attendre à avoir une composante fréquentielle dominante de 1/24 h = 0.042 h^-1 qui traduit simplement le fait qu'il fait habituellement plus chaud le jour (avec un maximum aux alentours de midi) et plus frais la nuit (avec un minimum à un moment donné de la nuit). Donc, si l'on considère une période où le temps reste stable, par exemple une semaine, nous pouvons approximer les variations de température en fonction du temps par une onde sinusoïdale ayant une période de 24 h. Si nous effectuons la transformation de Fourier sur cette onde sinusoïdale, nous constatons qu'elle ne contient qu'une seule fréquence (affichée sous la forme d'une fonction δ) d'une fréquence 0,042h^-1. Voilà, c'est suffisant pour le cas simple, parce que si tout était aussi facile, nous n'aurions pas besoin de la transformée de Fourier. Nous allons plutôt passer à un cas plus complexe dans lequel l'intuition ne suffit pas.

Les données que nous utiliserons dans cet exemple sont les mesures de l'activité des taches solaires de l'année 1700 à l'année 2004 fournies par le National Geophysical Data Center - NOAA Satellite and Information Service. L'ensemble de données correspond aux observations annuelles des taches solaires disponibles via FTP ici. Elles se trouvent également dans le fichier taches_solaires.dat. Ces mesures ont servi à illustrer les performances de la FFT pour trouver une périodicité dans l'activité des taches solaires avec plusieurs langages de programmation, par exemple Matlab et BASIC. Les observations selon lesquelles il y a (ou il pourrait y avoir) une corrélation entre l'activité des taches solaires et la température du globe ont donné lieu à une controverse lorsqu'on parle de l'effet de serre et du réchauffement climatique.

Le graphe ci-dessous illustre les données de taches solaires à utiliser dans cet exemple.

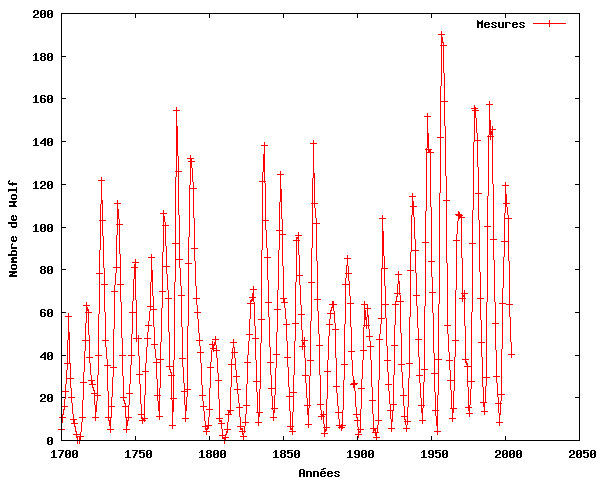
Le code ci-dessous présente le script permettant d'analyser les données de taches solaires. Il s'agit d'une version abrégée, dont plusieurs tracés ont été supprimés. Le script complet se trouve dans taches_solaires.py.txt.

     0  # -*- encoding:iso-8859-1 -*-
     1  from scipy import *
     2  import scipy.io.array_import
     3  from scipy import gplt
     4  from scipy import fftpack
     5  
     6  tempdata = scipy.io.array_import.read_array('taches_solaires.dat')
     7  
     8  annees=tempdata[:,0]
     9  wolf=tempdata[:,1]
    10  Y=fft(wolf)
    11  n=len(Y)
    12  puissance = abs(Y[1:(n/2)])**2
    13  nyquist=1./2
    14  freq=array(range(n/2))/(n/2.0)*nyquist
    15  periode=1./freq
    16  gplt.plot(periode[1:len(periode)], puissance,'title "Mesures" with linespoints')
    17  gplt.xaxis((0,40))
    18  gplt.xtitle('Période [an]')
    19  gplt.ytitle('|FFT|**2')
    20  gplt.grid("off")
    21  gplt.output('taches_solaires_periode.png','png medium transparent size 600 400')

Dans les premières lignes, nous importons tous les paquetages nécessaires. Dans la ligne 6, les données de taches solaires sont importées et stockées dans la variable tempdata. Pour des raisons de simplicité, les valeurs x (les années) et les valeurs y (le nombre de Wolf) sont stockées dans des variables séparées. Dans la ligne 10, nous effectuons la transformation de Fourier (FFT) sur les données de taches solaires. Comme le montre la figure ci-dessous, la sortie est un ensemble de nombres complexes (définissant à la fois l'amplitude et la phase des composantes fréquentielles), avec une symétrie apparente autour de l'axe Im=0.

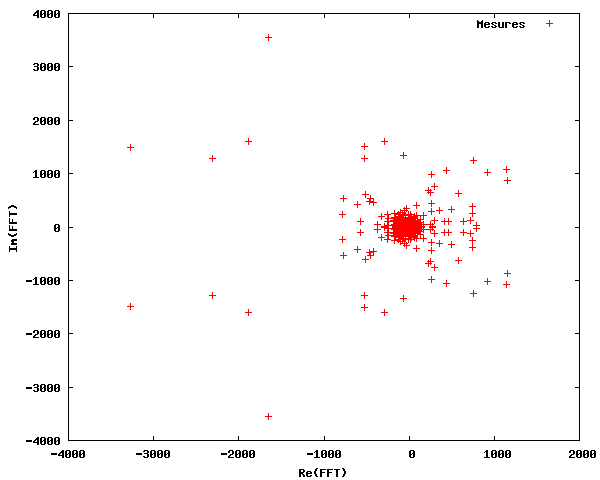
Pour construire un chronogramme, c'est-à-dire un graphe de la puissance en fonction de la fréquence, calculons d'abord la puissance du signal de la FFT, qui est tout simplement égale au carré du signal de la FFT. Nous n'avons besoin que de la partie du signal comprise entre 0 et une fréquence égale à la fréquence de Nyquist, laquelle est égale à la moitié de la fréquence maximale, du fait que les fréquences situées au-dessus de la fréquence de Nyquist correspondent à des fréquences négatives. La plage de fréquences est calculée de 0 à N/2 par N/(2T), où N est le nombre d'échantillons et T la période d'échantillonage. La figure ci-dessous présente le chronogramme obtenu.

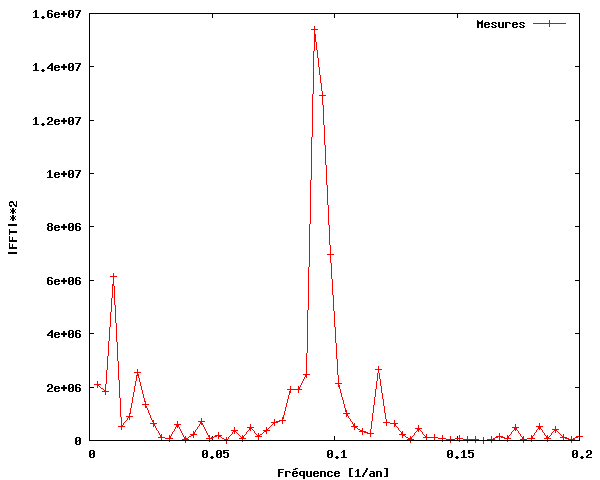
Ainsi, nous pouvons constater qu'il y a effectivement une périodicité dans l'activité des taches solaires, d'une fréquence d'environ 0,09. Notez que c'est plus facile à voir si nous utilisons la période (inverse de la fréquence) au lieu de la fréquence sur l'axe des x.

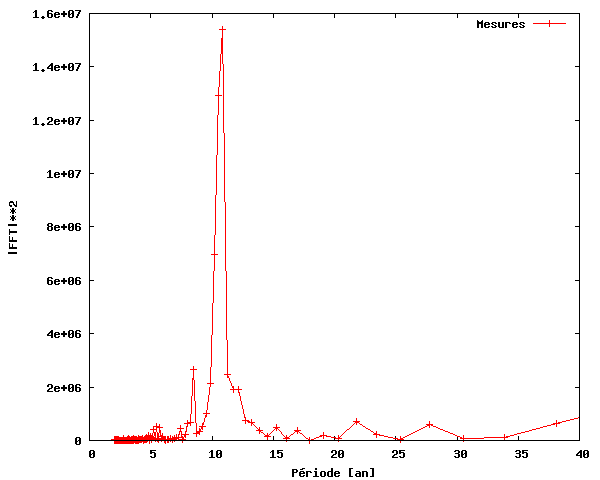
Comme on le voit sur cette figure, nous avons découvert (comme beaucoup d'autres) que l'activité des taches solaires de 1700 à 2004 est périodique et que les taches solaires se produisent avec une activité maximale environ tous les 11 ans.

Le prochain et dernier exemple est un peu plus complexe que les précédents. Sa tâche consiste à parcourir un certain nombre de fichiers de données (similaires à ceux utilisés dans l'exemple n°3 de la première partie et de prendre une tranche de chaque fichier de données correspondant à un pic de diffractométrie de rayons X^[5], comme représenté dans l'exemple n°2 de la première partie. Il est possible d'ajuster sur ce pic une courbe gaussienne (en cloche)^[6], dont les paramètres devront être stockés dans un fichier de données. Les paramètres extraits sont : position du pic, hauteur du pic et largeur du pic, qui tous contiennent des informations utiles sur l'échantillon en cours de test (MgH₂, un autre matériau pour le stockage de l'hydrogène à l'état solide). La position du pic est liée au réseau cristallin du matériau (en fait l'espacement inter-atomique, pour être précis), la hauteur du pic correspond à la quantité de matériau présent et la largeur du pic correspond à la taille des domaines cristallins de MgH₂. De plus, le script devrait admettre deux arguments en ligne de commande, trace et param, permettant respectivement de tracer l'ajustement des pics lorsque le script parcourt les fichiers de données et d'afficher les paramètres d'ajustement à l'écran. Cette fonction est surtout de nature diagnostique. Il faut également une sorte de mécanisme pour évaluer la qualité de l'ajustement et le disqualifier s'il est trop mauvais. Enfin, les scripts devraient générer un tracé des paramètres d'ajustement en fonction du temps (numéro de cycle). La longueur de ce programme approche 100 lignes et ne sera donc pas présenté ici, mais vous le trouverez dans le fichier lgtixrpd.py.txt. Dans la section suivante, nous parcourrons les parties principales de ce script. Pour exécuter l'exemple vous-même, vous devez également télécharger et décompresser les fichiers de données.

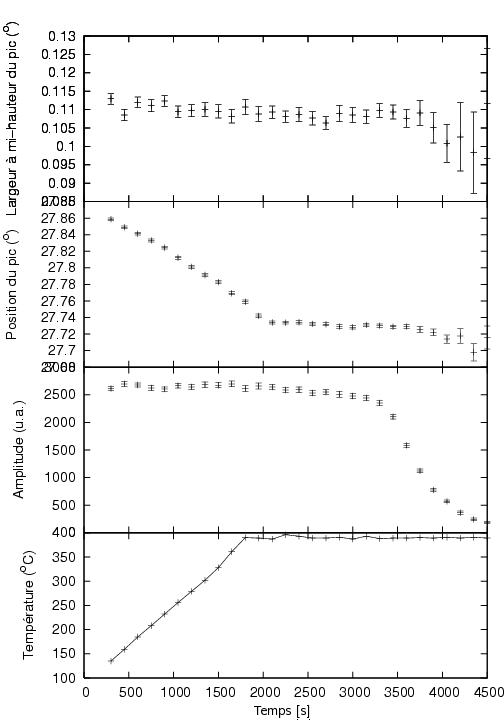
La figure ci-dessous illustre le tracé créé. D'après ce tracé, nous remarquons que durant l'échauffement (linéaire) de notre échantillon, la position du pic se décale vers des valeurs inférieures. D'après la Loi de Bragg sur la diffraction^[7], il y a une relation inverse entre la position des pics et l'espacement du réseau cristallin. Nous pouvons donc en conclure que notre échantillon se dilate pendant l'échauffement (comme on pouvait s'y attendre). Nous observons également que quand l'échantillon est porté à 400°C pendant un certain temps, l'amplitude commence à décroître, ce qui traduit la disparition du MgH₂ en raison de la décomposition qui accompagne la libération de l'hydrogène.

Dans cet article, quelques exemples ont été donnés afin d'illustrer que Python est effectivement un outil puissant pour la visualisation et l'analyse de données scientifiques. Il combine la puissance de tracé de courbes de gnuplot avec la puissance d'un véritable langage de programmation. Le paquetage SciPy comprend de nombreux outils scientifiques pour l'analyse de données.

Manuels, tutoriels, livres, etc. :

Consultez également les articles présents sur Python publié dans la Linux Gazette ^[8].