Cela fait 15 ans que j'utilise gnuplot, et il constitue une partie indispensable de mes outils : un des programmes de ma panoplie dont je ne peux me passer.

À l'origine, j'utilisais gnuplot dans le cadre de mes travaux de recherches à l'université, en tant que chercheur en physique de la matière condensée. Mais bien plus tard, lorsque j'ai rejoint Amazon.com, j'ai recommencé à utiliser gnuplot, mais cette fois-ci pour analyser le déplacement des employés au sein des gargantuesques entrepôts d'Amazon et la distribution de colis aux clients. Plus tard encore, j'ai découvert que gnuplot était très utile durant la période où j'étudiais les variations du trafic web pour la compagnie Walt Disney.

Je trouve gnuplot indispensable car il me permet de voir mes données, et ce, d'une manière facile et simple. En utilisant gnuplot, je peux dessiner et redessiner des graphiques, et voir les données de différentes façons. Je peux générer des images d'ensembles de données contenant des millions de points, et je peux écrire des scripts afin que gnuplot me crée des graphes automatiquement.

Ces choses ont de l'importance. Durant l'une de mes missions, j'ai pu découvrir des informations pertinentes car j'ai pu générer littéralement des centaines de graphes. En les mettant tous sur une page Web, les uns à côté des autres, de flagrantes similitudes (et différences) entre différents ensembles de données sont apparues, chose qui n'avait jamais été remarquée auparavant, notamment parce que, à part moi, tout le monde utilisait d'autres outils (Excel surtout) qui permettaient de ne créer qu'un graphe à la fois.

Gnuplot a toujours été très prisé par les scientifiques partout dans le monde. J'espère vous convaincre qu'il peut être utile à un public beaucoup plus large : analystes d'entreprise, directeurs des opérations, administrateurs de bases de données et d'entrepôts de données, programmeurs, en fait toute personne souhaitant comprendre des données à l'aide de graphes.

J'aimerais vous montrer comment faire.

Gnuplot est probablement le programme open-source le plus largement utilisé pour porter des données sur un graphique et les visualiser. Dans ce document, je veux vous montrer comment utiliser gnuplot pour représenter vos données par des tracés et des graphiques : aussi bien des graphes faciles et rapides pour votre utilisation personnelle que des graphes très soignés pour des présentations ou des publications.

Mais je souhaite aussi vous montrer quelque chose d'autre : comment résoudre des problèmes d'analyse de données par des méthodes graphiques. L'art de découvrir les relations liant les données et d'en tirer des informations visuellement s'appelle « l'analyse graphique ». Je considère gnuplot comme un excellent outil pour faire cela.

Pour vous donner un aperçu, prenons quelques problèmes et voyons comment nous pourrions les aborder en utilisant des méthodes graphiques. Les graphes, ici et dans le reste du document (avec de très rares exceptions), ont été, naturellement, générés avec gnuplot.

Pour se rendre compte des types de problèmes auxquels nous pourrions être confrontés, ainsi que les types de solutions que gnuplot peut nous aider à trouver, étudions deux exemples. Les deux ont lieu durant un week-end long et chargé.

Imaginez que vous êtes responsable de l'organisation du marathon de la ville. Il y aura plus de 2000 personnes engagées, la circulation sera interdite en ville, il y aura plein de spectateurs et une grande fête à l'arrivée en l'honneur des vainqueurs et pour aider les éclopés. La grande question est : quand les officiels chargés de la ligne d'arrivée devront-ils être prêts à accueillir la majorité des coureurs ? A quel moment prévoit-on l'afflux en masse ?

Vous avez à votre disposition les résultats du marathon de l'année dernière. En supposant que les coureurs ne se sont pas améliorés sensiblement durant l'année passée (probablement une hypothèse sans risque !), vous faites une moyenne rapide du temps qu'il a fallu à ces derniers pour achever leur course et vous trouvez que la moyenne de l'an dernier était 172 minutes. Pour garder une marge, vous calculez également l'écart-type, ce qui donne environ 15 minutes. Donc vous dites à votre équipe d'être prête pour le grand rush qui commencera deux heures et demie (150 minutes) après le départ, et vous vous dites que cela devrait se passer à peu près bien.

Mais vous êtes quelque peu surpris lorsque, le jour J, plein de coureurs commencent à se montrer à la ligne d'arrivée au bout de seulement 130 minutes : une bonne vingtaine de minutes avant le début du rush prévu à l'origine. Dans le cas de l'organisation d'une manifestation de ce genre, une erreur de 20 ou 30 minutes n'est pas vraiment catastrophique, quoiqu'un peu bizarre. Le lendemain, vous vous demandez : qu'est-ce qui n'a pas tourné comme prévu ?

Regardons les données pour voir la leçon que nous pouvons en tirer. Jusqu'ici, tout ce que nous en connaissons est la moyenne et l'écart-type.

La moyenne est pratique : elle est facile à calculer et elle résume la totalité de l'ensemble de données en un seul chiffre. Mais en calculant la moyenne, nous avons perdu beaucoup d'informations. Pour comprendre tout l'ensemble de données, il faut pouvoir visualiser. Et comme nous ne pouvons pas comprendre des données en regardant plus de 2000 temps de parcours individuels, cela signifie que l'on doit les représenter par un tracé.

Il sera pratique de regrouper les coureurs en fonction de leur temps de parcours et de compter le nombre de participants ayant achevé leur course à chaque intervalle d'une minute. On obtient alors un fichier commençant comme ceci :

Maintenant, traçons le nombre de coureurs en fonction du temps de parcours.

Figure 1. Nombre d'arrivants en fonction du temps (en minutes)

Nous voyons immédiatement où nous nous sommes trompés : les données sont bimodales, ce qui veut dire qu'elles ont deux pics. Il y a un premier pic a environ 150 minutes et un autre grand pic à 180 minutes.

En fait, cela s'explique bien : un important évènement sportif comme le marathon de la ville attire deux groupes très différents de personnes : les « athlètes », qui s'entraînent et participent à des compétitions durant toute l'année et viennent pour gagner, et un groupe bien plus grand « d'amateurs », qui viennent une fois par an pour un grand évènement et sont surtout présents pour participer.

Le problème est que pour de telles données, la moyenne et l'écart-type sont évidemment de mauvaises représentations, à tel point qu'au moment où on attendait le grand rush (170 minutes), il y avait en fait une petite accalmie au niveau de la ligne d'arrivée !

La leçon à en tirer ici est qu'en général il vaut mieux éviter de se fier à des statistiques sommaires (comme la moyenne) pour des ensembles inconnus de données. Il faut toujours voir à quoi ressemblent les données. Une fois qu'on a vérifié la forme globale, on peut choisir comment récapituler au mieux nos constatations.

Et bien sûr, on peut toujours en apprendre plus. Dans cette étude, par exemple, nous voyons qu'après environ 200 minutes, presque tout le monde a fini, et on peut commencer à lever le pied. La « queue » de la distribution est assez petite ; en fait, cela est un peu surprenant (je me serais attendu à voir un plus grand nombre de vrais « retardataires », mais il se peut que beaucoup parmi les coureurs qui sont vraiment lents ont abandonné la course quand ils se sont rendus compte qu'ils termineraient en bas du classement).

Regardons la commande gnuplot qui a été utilisée pour générer la figure 1.1. Gnuplot est orienté lignes de commande : après le démarrage de gnuplot, on arrive dans une session interactive de commande, et toutes les commandes sont tapées dans l'affichage interactif de gnuplot.

Gnuplot lit les données dans des fichiers textes ordinaires, les données étant organisées en colonnes comme montré précédemment. Tracer des données contenues dans un fichier ne nécessite qu'une seule commande : plot, comme ceci :

plot "marathon" using 1:2 with boxes

Pour la commande plot, on utilise le nom du fichier comme argument, entre guillemets. Le reste de la ligne de commande indique quelles colonnes utiliser pour le tracé, et de quelles manières représenter les données. La déclaration using 1:2 spécifie à gnuplot de prendre la première et la deuxième colonne dans le fichier appelé marathon. La dernière partie de la commande : with boxes, permet la sélection du style de boîte, ce qui convient souvent pour afficher un dénombrement d'évènements, comme dans notre cas.

Gnuplot gère presque tout le reste par lui-même : il dimensionne les graphes et sélectionne l'échelle la plus intéressante, il dessine les bordures, et il place les points ainsi que leurs indications. Tous ces détails sont modifiables, mais le plus souvent gnuplot anticipe très bien sur les besoins de l'utilisateur.

Détermination du futur

Ce weekend-là, pendant que 2000 coureurs font la course en ville, un doctorant assidu travaille sur son sujet de recherche. Il étudie l'Agrégation Limitée par Diffusion [DLA, Diffusion Limited Aggregation], un processus dans lequel une particule effectue un mouvement Brownien, jusqu'à ce qu'elle arrive au contact d'un « amas » de particules en formation. Au moment du contact, la particule s'accroche à l'amas, au point d'impact, et devient une partie de celui-ci. Puis une nouvelle particule, suivant elle aussi un mouvement Brownien, se met en route jusqu'à ce qu'elle s'agglutine à l'amas. Et ainsi de suite.

La structure des amas ayant grandi au cours de ce processus est remarquablement ouverte et mince (cf. figure 1.2). Les amas de DLA sont des fractales dont on a une connaissance encore assez floue.[1]

Figure 2. Un amas DLA de N=30000 particules, dessiné avec gnuplot.

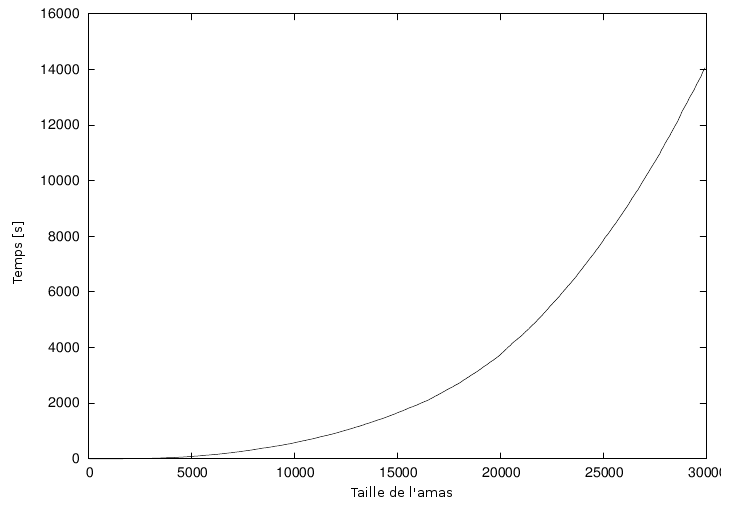
Le processus du DLA est très simple, et donc, apparemment, écrire un programme permettant de construire de tels amas sur un ordinateur n'a rien de compliqué, et notre dynamique doctorant s'y est mis. Au départ, tout semblait fonctionner, mais au fur et à mesure que la simulation progressait, l'amas de particules semblait grandir de moins en moins vite. Le ralentissement en devenait insupportable. Le but était de faire grandir un amas de DLA de N=100000 particules : le programme se terminerait-il un jour ?

Fort heureusement, le programme de simulation écrit régulièrement dans un journal des informations concernant sa progression : pour chaque nouvelle particule ajoutée à l'amas, le temps passé (en secondes) depuis le début de la simulation est enregistré. Nous devrions être capables de prévoir le temps requis pour achever la construction à partir de ces données, mais un premier graphique (figure 1.3) n'aide pas réellement : il y a tout simplement trop de manières différentes d'extrapoler cette courbe pour des tailles plus grandes d'amas.

Figure 3. Temps nécessaire pour construire un amas DLA.

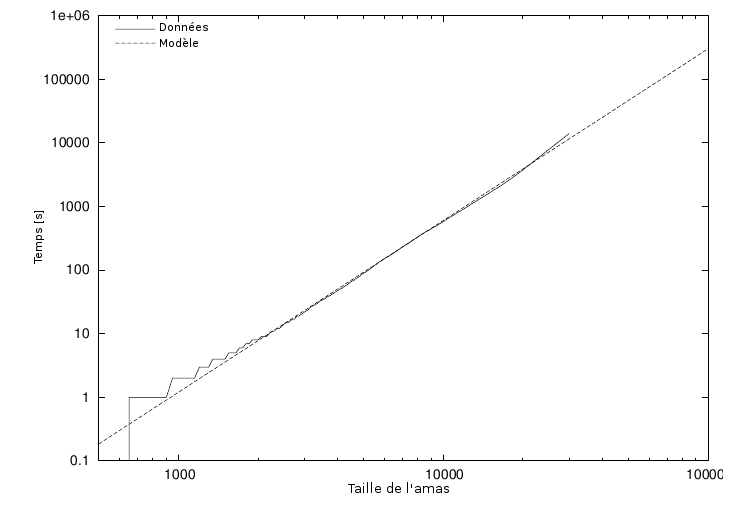
Cependant, le temps utilisé par les algorithmes croît comme une puissance de la taille du problème. Dans notre cas, ce serait le nombre N de particules dans l'amas : T ~ N^k, pour une certaine valeur k. Notre étudiant-chercheur a donc tracé le temps d'exécution de sa simulation en fonction de la taille de l'amas, sur une échelle logarithmique : et voilà, les données suivent une ligne droite, ce qui traduit une évolution en loi de puissance. (J'expliquerai plus tard comment et pourquoi ça marche). De façon empirique, il trouve aussi une équation qui approxime assez bien les données. Cette équation peut être utilisée sur n'importe quelle taille d'amas voulue et donnera le temps nécessaire. Pour N=100000 (qui était le but visé à l'origine), nous pouvons lire T=300000 secondes (ou plus), ce qui correspond à 83 heures ou quatre jours. Nous pouvons donc dire à notre ami qu'il est inutile de passer tout son weekend dans le laboratoire ; il devrait sortir (peut-être faire un marathon), et revenir lundi. Ou peut-être concevoir un meilleur algorithme. (Pour les simulations de croissance d'amas de DLA, des améliorations spectaculaires en terme de vitesse sont possibles par rapport à une mise en œuvre simpliste. Essayez si vous le souhaitez).

Figure 4. Temps nécessaire pour construire un amas DLA tracé sous une échelle logarithmique, avec un modèle mathématique approché.

Utilisation de gnuplot

Regardons à nouveau comment les graphes de cette partie ont été créés. La manière la plus simple de comprendre est de regarder la figure 1.3. Avec un fichier contenant deux colonnes, une donnant la taille de l'amas et l'autre donnant le temps de construction, la commande est simplement :

plot "data" using 1:2 with lines

La seule différence par rapport à la figure 1.1 est la forme : plutôt que des boîtes, j'ai utilisé des segments de droites pour relier les différents points, d'où l'utilisation de with lines.

Avez-vous remarqué que les figures 1.3 et 1.4 contiennent plus que de simples données ? Les deux axes portent à présent des noms ! Les détails tels que légendes et autres décorations utiles font souvent la différence entre un graphe médiocre et un graphe de grande qualité car ils fournissent à l'observateur le contexte nécessaire pour comprendre parfaitement le graphe.

Dans gnuplot, tous les détails concernant l'apparence d'un graphe sont gérés en choisissant les bonnes options. Pour mettre des titres aux abscisses et ordonnées dans la figure 1.3, j'ai tapé :

set xlabel "Cluster Size"
set ylabel "Run Time [sec]"

La figure 1.4 est tracée en utilisant des axes à échelle logarithmique. C'est encore une autre option, qui est défini comme suit :

set logscale

La figure 1.4 montre deux courbes : les données ainsi que la meilleure « approximation ». Tracer plusieurs ensembles de données ou fonctions mathématiques en même temps sur un seul graphique est très simple : il suffit de les écrire l'un après l'autre sur la ligne de commande avec :

plot "runtime" using 2:6 title "data" with lines, #
#    1.2*(x/1000)**2.7 title "model"synonymes

Cette commande amène une autre fonction de gnuplot : la directive title. Elle prend une chaîne de caractères en argument, qui sera affichée avec le type de tracé dans la légende (visible dans le coin supérieur gauche de la figure 1.4).

Finalement, nous en venons à la figure 1.2. On n'a pas tout à fait la même bestiole, là. Vous remarquerez qu'il manque les bords et les croix marquant les données. Le format de l'image (la proportion de la largeur du graphe par rapport à sa hauteur) a été contraint à 1, et un seul point a été placé à la position de chaque particule de l'amas. Voici les commandes les plus importantes que j'ai utilisées :

unset border
unset xtics
unset ytics

set size square

plot "cluster" using 1:2 with dots

Vous voyez que gnuplot est très simple d'utilisation. Dans la partie suivante, j'aimerais parler d'avantage de l'utilisation de méthodes graphiques pour comprendre un ensemble de données, avant de revenir sur gnuplot et expliquer pourquoi il s'agit de mon outil favori pour ce genre d'activité.

Ces deux exemples ont dû vous donner une idée de ce qu'est l'Analyse Graphique et comment cela marche. Les étapes fondamentales sont toujours les mêmes :

Nous pouvons utiliser des choses plus sophistiquées, mais ceci est l'idée de base. Si l'hypothèse à la deuxième étape semble relativement bien justifiée, nous essayerons souvent d'annuler ses effets, par exemple, en soustrayant une formule des données, pour voir si on peut reconnaître un motif caractéristique dans les résidus. Et ainsi de suite.

L'itération est un aspect crucial de l'analyse graphique : tracer les données comme ceci ou comme cela, les comparer à des fonctions mathématiques ou à d'autres ensembles de données, zoomer sur des sections intéressantes ou faire un zoom arrière pour observer la tendance générale, appliquer un logarithme ou d'autres méthodes de transformations de données pour modifier son allure, utiliser un algorithme de lissage pour atténuer les bruits... Pendant une séance intense d'analyse où on utilise un nouveau jeu de données qui semble prometteur, il n'est pas inhabituel de produire littéralement des douzaines de graphes.

Aucun de ces graphes ne restera longtemps. C'est parce que ce sont des graphes de transition ne restant que le moment nécessaire pour nous permettre de déterminer une nouvelle hypothèse que nous essayerons de justifier dans un éventuel prochain graphique. Cela veut aussi dire que ces graphes ne seront en aucune façon « affinés » puisqu'ils sont l'équivalent graphique des brouillons, c'est-à-dire les notes d'un travail en cours destinées à notre usage personnel.

Cela ne veut pas dire qu'il est exclu que l'on affine les graphes. Mais ce sera pour plus tard dans le processus  une fois que nous connaissons les résultats de notre analyse, nous avons besoin de les communiquer aux autres. A ce moment-là, nous créerons des graphes « permanents », qui dureront pendant une période plus longue, peut-être jusqu'à la prochaine présentation de département, ou (si le graphe vient à être inclus dans une publication scientifique, par exemple) pour toujours !

On attend différentes choses de ces graphes qui resteront pour la postérité : ils doivent pouvoir être compris par d'autres, peut-être même dans plusieurs années, et il y a peu de chances que nous soyons là pour les expliquer. Ainsi, les éléments faisant partie du graphique comme les étiquettes, les légendes, et d'autres informations contextuelles deviennent très importantes. On doit comprendre tout de suite ce que le graphe est censé mettre en évidence. Les graphes de présentation doivent se suffire à eux-mêmes. Maintenant que nous connaissons les résultats de notre analyse, nous devons trouver le moyen le plus clair et le plus facilement compréhensible de présenter nos découvertes. Un graphe de présentation est censé mettre en évidence quelque chose et de façon correcte.

Finalement, certains diront qu'un graphe de présentation doit avoir « une bonne tête ». Peut-être. Si il parle bien de lui-même, il n'y a pas de raison pour laquelle il ne devrait pas être visuellement plaisant aussi. Mais cela, on y pense après coup. Même pour un graphe de présentation, l'important est le contenu, pas le contenant !

Gnuplot est un programme pour explorer les données graphiquement. Son but est de générer des tracés et des graphes à partir de données ou de fonctions. Il peut produire des graphes très travaillés, appropriés à la publication, et des graphes tracés rapidement qui servent simplement lorsque nous survolons une idée.

Gnuplot se gère en ligne de commande : on tape des commandes dans l'invite, et gnuplot redessine aussitôt le tracé en cours. Gnuplot est également interactif : la sortie est générée et affichée immédiatement dans une fenêtre de résultat. Bien que gnuplot puisse s'utiliser comme processus en arrière plan en mode de traitement par lots, l'utilisation standard est hautement interactive. D'un autre côté, ses principales interactions avec l'utilisateur se font par un langage de commande et non par une interface graphique permettant l'utilisation de la souris.

Ne laissez pas l'aspect langage de commande vous rebuter : gnuplot est facile d'utilisation, vraiment très facile d'utilisation ! Il suffit d'une seule ligne pour lire et tracer un fichier de données, et la majeure partie de la syntaxe des commandes est simple et plutôt intuitive. Gnuplot ne demande pas de connaissance en programmation ni une profonde compréhension de la syntaxe des commandes pour se lancer.

Alors, quel que soit le type de travail avec gnuplot, le processus de base est le suivant : tracer, examiner, répéter jusqu'à ce que vous ayez trouvé ce que vous vouliez apprendre des données. Gnuplot supporte parfaitement le processus itératif nécessaire au travail préparatoire !

Dans cet article, je vous ai montré deux ou trois exemples qui prouvent la puissance des méthodes graphiques pour comprendre des données. J'ai aussi essayé de suggérer des méthodes adaptées pour traiter les problèmes d'analyse de données : tracer les données, identifier les caractéristiques essentielles de l'ensemble de données à partir du graphe, et recommencer le processus pour faire ressortir le comportement qui vous intéresse le plus, et enfin (pas toujours, mais souvent) déterminer une description mathématique des données qui pourra ensuite être utilisée pour faire des prédictions (qui, par nature, vont au-delà des informations contenues dans les données en question).

Plusieurs banques de données sur le Web ont été très utiles, soit pour les jeux de données qui s'y trouvaient, soit parce qu'elles ont simplement constitué une source d'inspiration. Parmi les plus utiles, il y avait :

[1] L'article original concernant la DLA était « Diffusion Limited Aggregation, A Kinetic Critical Phenomenon » (L'Agrégation Limitée par Diffusion, un Phénomène Cinétique Critique) par T. A. Witten et L. M. Sander ; il fût publié dans la Physical Review Letters Vol. 41, p. 1400 en 1981. Il s'agit de l'un des articles les plus cités de tous les temps dans ce journal. Si vous voulez en apprendre plus sur la DLA et les processus similaires, vous pouvez lire Fractals, Scaling, and Growth Far From Equilibrium de Paul Meakin (1998)