Recherche de motifs avec les expressions rationnelles en C++ Par Oliver Mëller. Adaptation française : Éric Jacoboni. Précédent Suivant Table des Matières 2. Recherche de motifs avec les expressions rationnelles en C++ Les expressions rationnelles sont le moyen le plus souple pour rechercher des « motifs » de texte (groupe de caractères exprimant des critères). Depuis plus de vingt ans, elles sont utilisées dans plusieurs outils UNIX. Le but de cet article est de vous guider dans l'implantation de cette technique de recherche UNIX de base en C++. Tous ceux qui ont travaillé sur un système UNIX connaissent l'utilité des expressions rationnelles. On les trouve dans grep, awk ou Emacs, par exemple, et elles permettent de spécifier facilement des motifs de recherche. Toute personne ayant déjà utilisé un outil comme grep ne voudrait pas perdre sa souplesse - qui le voudrait ? La large utilisation d'outils de recherche comme grep vient des expressions rationnelles. Ôtez de grep cette technique de recherche par motifs, remplacez-la par un autre algorithme de recherche, Boyer-Moore, par exemple et l'outil que vous aurez sera un jouet - un jouet rapide, mais un jouet ! (l'outil find de MS-DOS en est un exemple...) Blague à part, les expressions rationnelles sont à la base de nombreux algorithmes de recherche dans de nombreux outils sous UNIX et donc aussi sous Linux. La puissance de cette technique de recherche est sans équivalent. Le but de cet article est l'implantation des expressions rationnelles dans une classe C++ réutilisable. Il sera votre guide et une introduction au monde fascinant de la « recherche par motifs » (pattern matching). 2.1 Principes Voyons d'abord quelques principes sur la recherche par motifs avec les expressions rationnelles. Pour indiquer un motif, il faut utiliser une notation qui puisse être traitée par un ordinateur. Cette notation, ou langage, est la syntaxe des expressions rationnelles. Le langage des expressions rationnelles est formé de symboles et d'opérateurs. Les symboles sont les caractères du motif. Pour décrire les relations entre ceux-ci, on utilise les opérateurs suivants (donnés dans l'ordre des priorités décroissantes) : Fermeture : une chaîne de symboles égaux de longueur variable ou un symbole optionnel (c'est le coeur même de la recherche par motifs). Concaténation : Si deux symboles se suivent dans le motif, les caractères correspondants doivent se suivre aussi dans le texte. Alternative : L'un des symboles de l'alternative doit apparaître dans le texte dans lequel le motif est recherché. En plus de ces opérateurs associatifs à gauche, on peut utiliser des parenthèses pour modifier les priorités des opérations. Dans beaucoup d'implantations des expressions rationnelles, les opérateurs de fermeture sont : l'astérisque (*), qui signifie une répétition de 0 à n occurences d'un symbole ; le plus (+), qui signifie une répétition de 1 à n occurences d'un symbole ; le point d'interrogation (?), qui signifie une éventuelle occurrence d'un symbole. Exemples : A* correspond à une chaîne vide, à « A », « AA », « AAA », etc. A+ correspond à « A », « AA », « AAA », etc. A? correspond à une chaîne vide ou à « A ». Pour indiquer une concaténation, on n'a pas besoin d'utiliser d'opérateur particulier. Une chaîne formée de tous les autres symboles est une concaténation. Par exemple, ABC correspond à « ABC ». Une alternative est décrite avec un | entre les deux expressions rationnelles possibles. A\B correspond à « A » ou à « B ». Dans les implantations étendues des expressions rationnelles, on utilise d'autres opérateurs pour décrire plus efficacement les motifs complexes. Cet article ne sera qu'une petite introduction aux possibilités syntaxiques et non une référence détaillée. 2.2 L'automate Pour rechercher un motif représenté par une expression rationnelle, vous ne pouvez comparer chaque caractère du motif et du texte. Avec la fermeture et à l'alternative, il y a tant de possibilités de motifs complexes qu'ils ne peuvent être tous trouvés par un algorithme « conventionnel ». On doit utiliser une technique plus efficace. La meilleure méthode est de construire et simuler un automate pour le motif. Pour décrire un motif de recherche décrit par une expression rationnelle, on peut utiliser des automates finis déterministes ou non déterministes. Un automate peut avoir plusieurs états. Il passe d'un état à l'autre en fonction d'un événement précis qui, ici, est le symbole ou caractère entré. La différence entre automate fini déterministe et non déterministe intervient ici. Un automate déterministe n'a qu'un état possible pour un symbole d'entrée donné, alors qu'un non déterministe pourra avoir plusieurs états suivants possibles pour le même symbole d'entrée. Les deux types d'automates peuvent être utilisés pour n'importe quelle expression rationnelle. Les deux ont leurs avantages et inconvénients. Le livre d'Aho, Ullman et Sethi : « Compilers, Principles, Techniques and Tools », publié par Addison-Wesley, est conseillé à tous ceux qui désirent en savoir plus sur ces types d'automates dans le contexte des expressions rationnelles (NdT : Complet, mais « trapu »). Dans notre implantation, nous utiliserons des automates non déterministes. C'est la stratégie la plus employée pour l'implantation des algorithmes de recherche par motifs et il est un peu plus facile de construire un automate non déterministe qu'un détermiste en se basant sur les expressions rationnelles. La figure 1 montre un diagramme de transition d'un automate fini non déterministe pour la reconnaissance du motif a*(cb|c*)d. Ce dernier contient tous les types d'opérations -- une alternative, deux fermetures et trois symboles concaténés. Remarquez que les parenthèses qui contiennent les symboles alternatifs ne compte que pour un symbole dans la concaténation. L'état initial est le rectangle situé à gauche, l'état final est le rectangle barré situé à droite.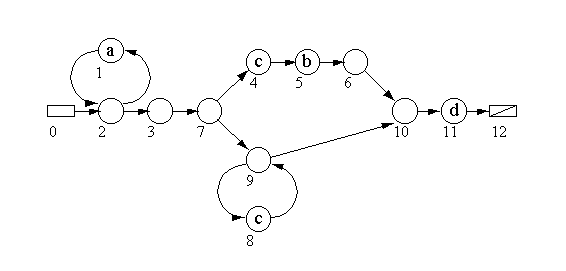 Figure 1. Automate fini non déterministe pour le motif a*(cd|c*)d. Ce petit motif et son automate mettent très bien en évidence les problèmes de la recherche par motifs. À l'état n°7, on ne sait pas quel sera l'état suivant pour le caractère d'entrée « c ». Les états 4 et 9 sont des possibilités. L'automate doit chercher -- pour trouver -- le chemin correct. Pour reconnaitre la chaîne « aaccd », par exemple, l'automate commencera par l'état n°0 -- l'état initial. L'état suivant, le n°2, est un état vide : cela signifie qu'aucun caractère ne doit correspondre pour atteindre cet état. Le premier symbole d'entrée est un « a ». L'automate passe dans l'état n°1 qui est la seule possibilité. Lorsque le « a » a été reconnu, le caractère d'entrée suivant est lu et l'état suivant est à nouveau le n°2. Pour le caractère d'entrée suivant, qui est aussi un « a », ces deux dernières étapes se répètent. Après cela, la seule possibilité est de passer dans l'état n°3 et 7. Nous sommes maintenant dans un état qui peut poser problème. L'entrée suivante est un « c » et nous voyons alors la véritable puissance de l'automate. Il peut trouver le bon chemin qui sera l'état n°9 et non le n°4. C'est l'âme de la stratégie non déterministe : les solutions possibles sont découvertes, elles ne sont pas décrites par un algorithme fonctionnant en « pas à pas ». Dans le monde réel de la programmation, on doit prouver tous les chemins possibles, bien sûr. Mais nous verrons l'aspect pratique un peu plus tard. Après la décision en faveur de l'état n°9, l'automate passe sur 9, 8 (le premier « c » correspond), 9, 8 (le second « c » correspond), 10 et 11 (le « d correspond) pour atteindre l'état n°12. L'état final a été atteind et le résultat est que le texte « aaccd » correspond au motif a*(cb|c*)d. 2.3 Conception Une implantation d'expression rationnelle peut toujours être divisée en un compilateur qui génère un automate pour le motif donné, et un interpréteur ou simulateur, qui simule l'automate et recherche le motif. Le coeur du compilateur est l'analyseur lexical qui se base sur la grammaire « context free » suivante : liste ::= élément | élément "|" liste élément ::= ( "(" liste ")" | v ) ["*"] [élément] Ce représentation EBNF (Extended Backus-Naur Form) décrit la grammaire (réduite) d'un expression rationnelle. Il n'est pas possible ici d'expliquer les grammaires context free ni l'EBNF et, si vous ne connaissez pas ces sujets, reportez-vous au livre d'Aho, Ullman et Sethi, déjà cité, ainsi qu'a celui de Sedgewick et Robert : « Algorithms », publié par Addison- Wesley, par exemple. Dans notre exemple d'implantation, nous n'implanterons que les opérateurs de base | et *. Nous n'implanterons pas les autres opérateurs de fermeture + et ?. Avec l'aide de la figure 2, ce ne sera pas un problème pour vous de les implanter aussi. La fonctionnalité complète pour les expressions rationnelles sera encapsulée dans la classe RegExpr. Elle contient le compilateur et l'interpréteur/simulateur. L'utilisateur n'a affaire qu'aux deux constructeurs, à un opérateur surchargé et quatre méthodes pour compiler, rechercher et pour la gestion des erreurs. Le motif peut être indiqué en appelant le constructeur RegExpr(const char *pattern), en utilisant l'opérateur d'affectation = ou la méthode compile(const char *pattern) method. Si re est objet de la classe RegExpr, les lignes suivantes configureront le motif a*(cb|c*)d : RegExpr re("a*(cb|c*)d"); ou RegExpr re; re = "a*(cb|c*)d"; ou RegExpr re; re.compile("a*(cb|c*)d"); Pour les recherches dans un tampon texte ou dans une chaîne, vous pouvez utiliser les méthodes search() et searchLen(). La différence entre les deux est que searchLen() attend un paramètre supplémentaire qui doit être une référence à une variable entiere non signée. La longueur de la sous-chaîne trouvée est retournée dans cette variable. Vous remarquerez que les fermetures, ainsi que l'alternative, font varier la longueur de la sous-chaîne trouvée : par exemple, a* trouve « » (chaîne vide), « a », « aa », etc. Dans des outils tels que grep, vous n'avez pas besoin de cette information supplémentaire. Vous pouvez utiliser search() à la place de searchLen(). Cette méthode est une simple méthode « inline » qui appelle searchlen() avec une variable « bidon ».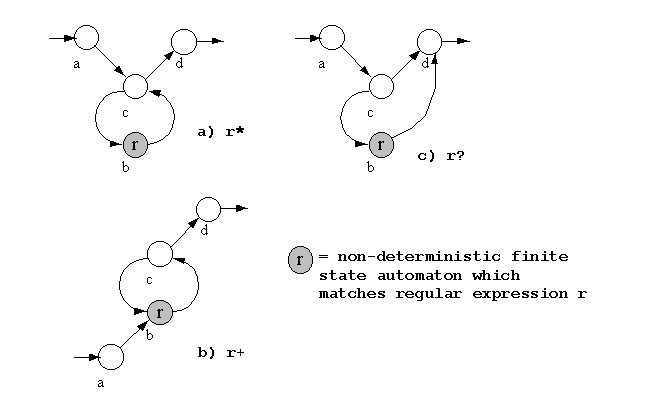 Figure 2. Automates pour l'implantation de la fermeture. La gestion des erreurs est complètement basée sur les exceptions. Si le compilateur indique une erreur de syntaxe dans l'expression rationnelle qu'il est en train de traiter, il lancera une exception de type xsyntax. Vous pouvez capturer celle-ci dans votre programme et appeler la méthode getErrorPos() qui retourne la position du caractère où l'erreur s'est produite. Ceci peut ressembler à ça : try { re.compile("a*(cb|c*)d"); } catch(xsyntax &X) { cout Une autre erreur qui peut survenir est « out of memory ». Cette erreur, provoquée par l'opérateur new, n'est pas traitée de la même façon par les compilateurs C++ actuels. gcc, par exemple, la traite par une terminaison du programme. D'autres lancent des exceptions. Les autres ne font absolument et attendent d'autres erreurs qui ne manqueront pas de survenir. Avec n'importe quel compilateur C++ ANSI, on résoud ce problème en utilisant la fonction set_new_errorhandler() (déclarée dans new.h) pour configurer une routine de gestion de cette erreur. Dans la plupart des cas; j'écris une petite routine pour lancer une exception qui indique ce type d'erreur et je la configure comme gestionnaire d'erreur de l'opérateur new. C'est, d'ailleurs, une solution facile pour programmer une gestion des erreurs portable qui puisse être utilisée par tous les compilateurs C++ ANSI et sous différents systèmes d'exploitation. Un objet RegExpr contient une méthode appelée clear_after_error() pour se nettoyer par lui-même lorsqu'une erreur est survenue, respectivement une exception a été lancée. Un appel à cette méthode est nécessaire car une erreur laisse le compilateur ou le simulateur dans un état indéfini qui peut provoquer des erreurs fatales lors d'autres appels de méthodes. 2.4 Le compilateur La grammaire montrée précédemment sous forme EBNF est implantée par les méthodes list, element et v. list et element. représentent les productions de l'EBNF. v est une méthode qui implante le symbole spécial v. Ce symbole signifie un caractère de la grammaire qui n'est pas un métacaractère (|, *, etc.). Il peut aussi être une séquence d'échappement comme \c, où c est n'importe quel caractère. En utilisant le backslash, la signification spéciale d'un métacaractère peut être annulée. Ces trois méthodes opèrent sur un tableau appelé automaton. Celui-ci est formé de structures contenant les informations sur les états de l'automate. Chaque entrée d'état contient les indices du (des) prochain(s) état(s) et le caractère qu'il doit reconnaître. Si l'état est un état vide, cette information sera un octet nul (\0).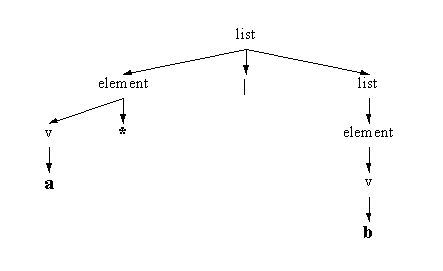 Figure 3. L'arbre d'analyse de « a*|b ». Notre implantation est un analyseur descendant (« top down »). Il utilise directement la stratégie récursive de la grammaire context free : chaque production est codée comme une fonction. L'analyseur divise le motif complet (l'expression rationnelle) en parties plus basses jusqu'à atteindre un symbole terminal. La figure 3 montre l'arbre d'analyse de « a*|b ». list est appelée d'abord et branche sur element non terminal, « | » terminal et list non terminale. element détecte v et « * », puis descend vers « a ». L'autre partie list descend directement à « b » en passant par element et v. L'arbre d'analyse de notre exemple d'expression rationnelle est montré figure 4.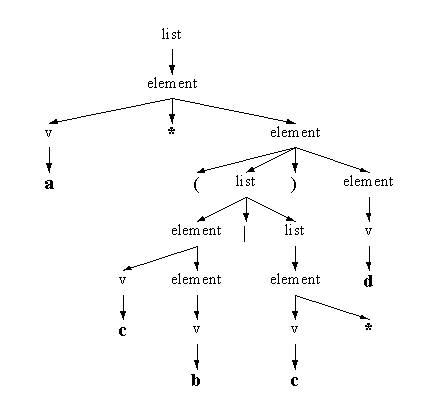 Figure 4. L'arbre d'analyse de « a*(cb|c*)d ». Tout symbole non terminal représente un appel de fonction dans notre analyseur. La stratégie descendante est la façon la plus facile d'implanter un analyseur à partir d'une grammaire context free (forme EBNF). Vous voyez que le plus important ici est d'avoir une spécification correcte de la grammaire ! Les états de l'automate sont générés à l'intérieur de ces méthodes. Un état sera créé pour chaque caractère de l'expression rationnelle. La seule exception est l'opérateur |, qui sera compilé en deux états. Les méthodes retournent toujours à l'appelant le point d'entrée (l'indice de l'état) vers l'automate partiel généré. La fin de l'automate partiel est toujours le dernier état courant dont l'indice est stocké dans l'attribut state de RegExpr. Les différents automates partiels sont montrés par la figure 5.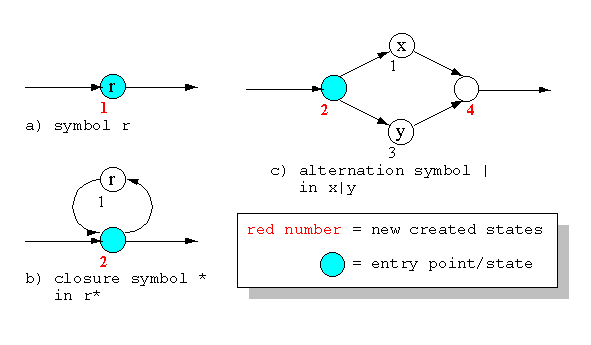 Figure 5. Un automate en plusieurs parties. Les nombres rouges indiquent les nouveaux états générés pour l'opération. La succession des nombres est définie par l'analyseur qui lit une chaîne de gauche à droite. Le point d'entrée, ou état, retourné est aussi marqué. Vous pouvez vous rendre compte qu'il est très important d'indiquer à la fonction où est le point d'entrée car ce n'est pas toujours celui ayant le plus petit index ! Les états, et l'ensemble de l'automate, sont générés de cette façon, étape par étape par un analyseur descendant. Il n'est pas utile d'en dire plus sur la création de l'automate, il est préférable de taper les sources, de les compiler et de voir l'algorithme en action en utilisant un debugger. Une petite remarque sur l'automate. Il est implanté dans RegExpr par la tableau statique automaton, ce qui est vraiment une implantation rudimentaire. Pour un programme réel et utile, vous devriez utiliser une meilleure stratégie : un objet agrégat de classe dans RegExpr fonctionnant avec un tableau dynamique, par exemple. Notez que cette implantation de l'automate peut provoquer des erreurs fatales si le motif est trop grand ! Elle n'a aucune fonction de vérification arrêtant la compilation du motif s'il n'y a plus d'états. Il n'est cependant pas difficile d'implanter l'automate comme une classe qui le gère dans un tableau dynamique ou une liste chaînée. 2.5 La simulation de l'automate Après la compilation du motif, on peut exécuter le code généré qui simule l'automate. L'intelligence de l'algorithme de recherche est implantée dans la méthode simulate(). Précédemment, on avait indiqué que l'automate trouvait la réponse correcte, mais d'un point de vue théorique. La simulation informatique d'un automate fini non déterministe doit prouver tous les chemins de correspondance possibles de cet automate. Sedgewick (voir son livre déjà cité), a implanté un algorithme intéressant qui réalise cette tâche. Notre algorithme partira de cette technique. Le système de Sedgewick possède quelques inconvénients pour une application réelle. Le premier est que sa grammaire nécessite un caractère après une fermeture sinon il ne peut la trouver. C'est un problème qui pourra être réglé par un patch qui doit venir bientôt et que notre implantation a déjà résolu. Le second problème est un peu plus complexe : l'implantation de Sedgewick s'arrête après avoir trouvé la première correspondance, ce qui signifie qu'elle ne trouve pas la chaîne de correspondance maximale. Par exemple, si l'on recherche « a*a » dans « xxaaaaaxx, elle ne trouvera que « a » au lieu de « aaaaa ». Notre implantation résoudra ce problème. L'idée qu'un programme puisse trouver le bon chemin peut sembler ridicule, mais le coeur d'un tel logiciel est de prouver tous les chemins possibles et de ne garder que le dernier comme étant le bon. Un traitement parallèle en est la clé. Chaque branche de l'automate sera testée et supprimée si elle ne convient pas. C'est un peu un méthode « essai et erreur ». Chaque chemin possible est testé en parallèle avec les autres et ôté lorsqu'il ne trouve pas le caractère courant traité par la recherche dans le texte. L'élément de base de cet algorithme est une double file (deque). Une double file est une file avec deux queues, c'est un hybride entre une pile et un tampon. On peut empiler et dépiler des données (pile) mais aussi en ajouter (tampon). En d'autres termes : vous pouvez ajouter des données en tête et en queue de cette structure. Ce comportement est important pour notre algorithme. La double file est divisée en deux parties : une partie supérieure pour le caractère couramment traité par la recherche dans le texte ; une partie inférieure pour le caractère suivant. Les représentations d'états suivants qui sont « vides » (ne rendent pas compte d'un état possible) sont stockées dans la partie supérieure car elles implantent la structure nécessaire à la détection d'une correspondance du caractère courant. Les valeurs des états suivant les états non vides (the_char != '\0') sont placées dans la partie inférieure car elles pointent sur le caractère suivant. Entre ces parties on stocke la valeur spéciale next_char (-1) qui indique que le caractère suivant du texte va être traité. La boucle principale de simulate() récupère un état de cette file et teste les conditions. Si le caractère dans le the_char de cet état correspond au caractère traité par la recherche, les indices des états suivants (next1 et next2) seront placés à la fin de la file. Si l'état lu est un état vide, les valeurs d'état suivantes seront placées au début. Si l'état est next_char (-1) le caractère suivant de la recherche sera traité. Dans ce cas, next_char est placé à la fin de la file. La boucle se termine lorsque l'on a atteint la fin du texte ou que la file est vide. Ce dernier cas intervient lorsqu'aucune partie correspondante n'est trouvée. Jusqu'à maintenant tout ceci ressemble à la version de Sedgewick, mais la différence est que lorsque l'état devient vide, la boucle ne se termine pas. Il est accepté comme un partie correspondante, cette information est stockée mais la boucle continue, ce qui rend possible la recherche d'autres correspondances ! Après la fin de la boucle, on retourne la dernière correspondance ou, si le motif n'a pas été trouvé, la position initiale de la recherche moins un. 2.6 Une petite application d'exemple Fichier regexpr.h : #ifndef __REGEXPR_H_OGM #define __REGEXPR_H_OGM class xsyntax { public: unsigned getErrorPos(){ return errorPos; } void setErrorPos(unsigned pos){ errorPos = pos; } protected: unsigned errorPos; }; #define MAXSTATES 100 class RegExpr { public: RegExpr(); RegExpr(const char *pattern); void compile(const char *pattern); int search(const char *str, unsigned start = 0); int searchLen(const char *str, unsigned &len, unsigned start = 0); const char *operator = (const char *pattern); void clear_after_error(); private: enum { no_error = 0, compiler_error, simulation_error }; short _error_type; void set_error_type(short et); protected: struct State { char the_char; unsigned next1, next2; } automaton[MAXSTATES]; void clear_automaton(); class Deque { public: Deque(); ~Deque(); void push(int n); void put(int n); int pop(); int isEmpty(); protected: struct Element { int n; Element *next; } *head, *tail; } deque; // compiler unsigned j, state; const char *p; unsigned list(); unsigned element(); unsigned v(); void error(); int isLetter(char c); // automaton simulation int simulate(const char *str, int j); }; inline const char *RegExpr::operator = (const char *pattern) { compile(pattern); return pattern; } inline int RegExpr::search(const char *str, unsigned start) { unsigned dummy; return searchLen(str, dummy, start); } // error codes of RegExpr::search and RegExpr::searchLen #define REGEXPR_NOT_FOUND -1 #define REGEXPR_NOT_COMPILED -2 #endif Fichier regexpr.cc : #include "regexpr.h" xsyntax _xsyntax; // RegExpr::Deque RegExpr::Deque::Deque() { head = 0; tail = 0; } RegExpr::Deque::~Deque() { while(head) { tail = head; head = head->next; delete tail; } } void RegExpr::Deque::push(int n) { Element *ptr = new Element; ptr->n = n; ptr->next = head; if(!tail) tail = ptr; head = ptr; } void RegExpr::Deque::put(int n) { Element *ptr = new Element; ptr->n = n; ptr->next = 0; if(!head) head = ptr; else tail->next = ptr; tail = ptr; } int RegExpr::Deque::pop() { int ret = head->n; Element *ptr = head; head = head->next; if(!head) tail = 0; delete ptr; return ret; } inline int RegExpr::Deque::isEmpty() { return head ? 0 : 1; } // RegExpr RegExpr::RegExpr() { automaton[0].next1 = 0; automaton[0].next2 = 0; } RegExpr::RegExpr(const char *pattern) { compile(pattern); } void RegExpr::clear_automaton() { for(int n=0;n<MAXSTATES;n++) { automaton[n].the_char = '\0'; automaton[n].next1 = 0; automaton[n].next2 = 0; } } // error handling void RegExpr::clear_after_error() { switch(_error_type) { compiler_error: clear_automaton(); break; simulation_error: while(!deque.isEmpty()) deque.pop(); } _error_type = no_error; } inline void RegExpr::set_error_type(short et) { _error_type = et; } // compiler inline int RegExpr::isLetter(char c) { return (c != '|' && c != '(' && c != ')' && c != '*' && c != '\\' && c != '\0' ? 1 : 0); } void RegExpr::compile(const char *pattern) { set_error_type(compiler_error); p = pattern; state = 0; j = 0; clear_automaton(); int n = list(); if(automaton[0].next1 == 0) automaton[0].next1 = automaton[0].next2 = n; automaton[state].next1 = automaton[state].next2 = 0; set_error_type(no_error); } unsigned RegExpr::list() { unsigned s1 = state++, s2 = element(), s3; if(p[j] == '|'){ j++; s3 = ++state; automaton[s3].next1 = s2; automaton[s3].next2 = list(); automaton[s3-1].next1 = automaton[s3-1].next2 = state; if(automaton[s1].next1 == s2 || automaton[s1].next1 == 0) automaton[s1].next1 = s3; if(automaton[s1].next2 == s2 || automaton[s1].next2 == 0) automaton[s1].next2 = s3; return s3; } return s2; } unsigned RegExpr::element() { unsigned s1 = state, s2; if(p[j] == '('){ j++; s2 = list(); if(p[j] == ')') { automaton[state].next1 = automaton[state].next2 = state+1; state++; j++; } else error(); } else s2 = v(); if(p[j] == '*') { automaton[state].next1 = s2; automaton[state].next2 = state+1; s1 = state; if(automaton[s2-1].next1 == s2 || automaton[s2-1].next1 == 0) automaton[s2-1].next1 = state; if(automaton[s2-1].next2 == s2 || automaton[s2-1].next2 == 0) automaton[s2-1].next2 = state; state++; j++; } else { if(automaton[s1-1].next1 == 0) automaton[s1-1].next1 = s2; if(automaton[s1-1].next2 == 0) automaton[s1-1].next2 = s2; } if(p[j] != '|' && p[j] != ')' && p[j] != '*' && p[j] != '\0') element(); return s1; } unsigned RegExpr::v() { unsigned s1 = state; char *s; if(p[j] == '\\') j++; else if(!isLetter(p[j])) error(); automaton[state].the_char = p[j++]; automaton[state].next1 = automaton[state].next2 = state+1; state++; return s1; } void RegExpr::error() { _xsyntax.setErrorPos(j); throw _xsyntax; } // automaton simulation int RegExpr::searchLen(const char *str, unsigned &len, unsigned start) { if(automaton[0].next1 == 0 && automaton[0].next2 == 0) return REGEXPR_NOT_COMPILED; set_error_type(simulation_error); int n, m, slen = strlen(str); for(n = start;n < slen;n++){ m = simulate(str, n); if(m < n - 1) { len = m - n + 1; set_error_type(no_error); return n; } } set_error_type(no_error); return REGEXPR_NOT_FOUND; } #define next_char -1 int RegExpr::simulate(const char *str, int j) { int state = automaton[0].next1, last_match = j - 1, len = strlen(str); if(automaton[0].next1 != automaton[0].next2) deque.push(automaton[0].next2); deque.put(next_char); do { if(state == next_char) { if(str[j]) j++; deque.put(next_char); } else if(automaton[state].the_char == str[j]) { deque.put(automaton[state].next1); if(automaton[state].next1 != automaton[state].next2) deque.put(automaton[state].next2); } else if(!automaton[state].the_char) { deque.push(automaton[state].next1); if(automaton[state].next1 != automaton[state].next2) deque.push(automaton[state].next2); } state = deque.pop(); if(state == 0) { last_match = j - 1; state = deque.pop(); } } while(j <= len && !deque.isEmpty()); return last_match; } #undef next_char Fichier eg.cc : #include <new.h> #include <iostream.h> #include <fstream.h> #include "regexpr.h" class xalloc {} _xa; void new_error() { throw _xa; } int main(int argc, char *argv[]) { if(argc != 2 && argc != 3) { cerr << "Usage: " << argv[0] << " pattern [file]" << endl; return 1; } ifstream in(0); if(argc == 3) { in.close(); in.open(argv[2]); if(!in) { cerr << argv[0] << ": Can't open " << argv[2] << endl; return 1; } } set_new_handler(new_error); RegExpr re; try { re.compile(argv[1]); int n; char buffer[500]; while(!in.eof()) { in.getline(buffer, 500); n = re.search(buffer); if(n >= 0) cout << buffer << endl; } } catch(xalloc exception) { cerr << endl << "Not enough memory." << endl; re.clear_after_error(); return 1; } catch(xsyntax syntax) { cerr << endl << "Syntax error near character position " << syntax.getErrorPos() << endl; re.clear_after_error(); return 1; } return 0; } Voici le fichier Makefile : OBJ = eg.o regexpr.o eg: $(OBJ) c++ -fhandle-exceptions -o eg $(OBJ) .cc.o: c++ -fhandle-exceptions -c $*.cc eg.o: eg.cc regexpr.h regexpr.o: regexpr.cc regexpr.h eg.cc est une implantation légère d'egrep. Il montre l'utilisation et la puissance de RegExpr. eg lit à partir de l'entrée standard, ou à partir d'un fichier spécifié en option, et imprime chaque ligne contenant le motif : Usage: eg motif [fichier]. RegExpr n'est, bien sûr, pas parfait dans cette implantation minimale, mais c'est une bonne base d'expériences. Certains points peuvent être modifiés ou ajoutés : fermetures ? et + ; implantation de l'automate comme un objet avec un tableau dynamique ou une liste chaînée pour la gestion des états ; classes de caractères [...] ; métacaractère . correspondant à tout caractère ; autres opérateurs de sed ou ed {...} métacaractères de début et fin de ligne ^ et $. J'espère que vous apprécierez cette implantation. Si vous avez des suggestions, des questions ou des idées, faites-m'en part. 2.7 Bibliographie Aho, Alfred V. Sethi, Ravi Ullman, Jeffrey D. : Compilers Principles, Techniques and Tools. Reading (Mass.) : Addison Wesley 1986 ; Mëller, Oliver : Mustererkennung mit Delphi-Suchen und Ersetzen von regulaeren Ausdruecken. mc extra (DOS International) 7/96 ; Sedgewick, Robert : Algorithms. Reading (Mass.) : Addison Wesley 2nd Ed. 1992 Copyright © 1998, Oliver Mëller - Publié dans le n°27 de la Linux-Gazette Adaptation française : Éric Jacoboni. Précédent Suivant Table des Matières Copyright © 1998, Oliver Mëller - Publié dans le n°27 de la Linux-Gazette Adaptation française : Éric Jacoboni.