Explorations mathématiques avec Scilab/Linux

1. Qu'est-ce que Scilab ?

Scilab est un environnment puissant et libre dédié au calcul mathématique. Il fournit un cadre extensible pour la manipulation générale des matrices et des « boîtes à outils » permettant d'effectuer des tâches comme la conception de systèmes de commande, le traitement du signal numérique, etc. Le code source C/Fortran est disponible en téléchargement sur la page d'accueil du projet — je n'ai eu absolument aucune difficulté à compiler le système — la magie des commandes configure, make, make install standard a parfaitement fonctionné.

Voici une capture d'écran de Scilab s'exécutant sur ma machine Linux :

2. Mathématiques simples

Commençons par quelques manipulations de matrices simples. Une matrice 3 x 3 est créée en saisissant simplement, à l'invite de Scilab :

-->a = [1,10,20; 5,6,7; 12,11,45]
 a  =
 
!   1.     10.    20. !
!   5.     6.     7.  !
!   12.    11.    45. !
 
-->

Il est facile d'obtenir la matrice transposée :

--->a'
ans  =
 
!   1.     5.    12. !
!   10.    6.    11. !
!   20.    7.    45. !
 
-->

Quelques autres fonctions :

-->sum(a, 'c')
 ans  =
 
!   31. !
!   18. !
!   68. !
 
-->sum(a, 'r')
 ans  =
 
!   18.    27.    72. !
 
-->diag(a)
 ans  =
 
!   1.  !
!   6.  !
!   45. !
 
-->

Les éléments peuvent être extraits des matrices de diverses manières — la plus simple est la procédure d'indexation standard. Écrire a(1,2) placerait l'élément à la ligne 1 et à la colonne 2 (notez que l'indice commence à 1). L'indexation d'une matrice au-delà de sa limite entraînera une erreur. Le fait d'écrire dans un indice non existant aboutit à l'extension dynamique de la matrice.

-->a(3,4) = 3
 a  =
 
!   1.     10.    20.    0. !
!   5.     6.     7.     0. !
!   12.    11.    45.    3. !
 
-->

3. L'opérateur « : »

Le petit opérateur « : » est intéressant car il nous permet de créer un vecteur des nombres 1,2,3 ... 10 en écrivant simplement :

-->a = 1:10
 a  =
 
!   1.    2.    3.    4.    5.    6.    7.    8.    9.    10. !
 
-->

Beaucoup d'autres astuces sont possibles :

-->b
 b  =
 
!   1.    2.    3. !
!   4.    5.    6. !
!   7.    8.    9. !
 

-->b(1:3,2:3)
ans  =
 
!   2.    3. !
!   5.    6. !
!   8.    9. !
 
-->1:2:10
 ans  =
 
!   1.    3.    5.    7.    9. !
 
-->

Notez que 1:2:10 équivaut à créer un vecteur commençant à partir de 1, chaque élément successif étant calculé en ajoutant 2, jusqu'à ce que la valeur devienne supérieure à 10.

4. Graphiques simples

Examinons un exemple de tracé d'onde sinusoïdale simple. Nous voulons un cycle complet de la courbe sinusoïdale (de 0 à 2*PI) : prenons 240 points entre les deux, de façon à ce que chaque division donne 2*PI/240. Créons d'abord un vecteur contenant toutes les valeurs d'angles dans cet intervalle, puis représentons-le graphiquement (%pi est une constante représentant la valeur de PI) :

--> = 0:(2*%pi)/240:2*%pi
 x  =
         column 1 to 5
 
!   0.    0.0261799    0.0523599    0.0785398    0.1047198 !
 
         column 6 to 9
 
!   0.1308997    0.1570796    0.1832596    0.2094395 !
 
         column 10 to 13
 
!   0.2356194    0.2617994    0.2879793    0.3141593 !
 
         column 14 to 17
 
!   0.3403392    0.3665191    0.3926991    0.4188790 !
[More (y or n ) ?] 

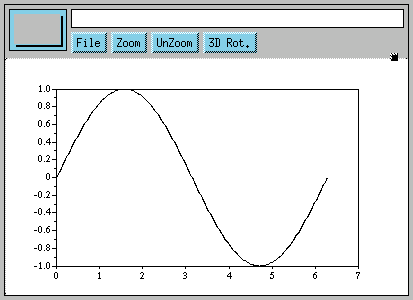
Utilisons à présent une fonction graphique simple :

-->plot(x, sin(x))

5. Écriture de scripts Scilab

L'écriture de scripts Scilab est simple. Voici un exemple de boucle for que l'on peut saisir à l'invite de Scilab proprement dit :

-->s = 0         
 s  =
 
    0.  
 
-->for i=1:3:10
-->  s = s + i
-->end
 s  =
 
    1.  
 s  =
 
    5.  
 s  =
 
    12.  
 s  =
 
    22.  
[More (y or n ) ?] 

6. Définition de fonctions

La syntaxe de la définition d'une fonction est un peu plus complexe. En voici un exemple simple :

-->function [r] = my_sqr(x)
-->  r = x * x
-->endfunction
 
-->my_sqr(3)
 ans  =
 
    9.  
-->

Après le mot-clé function, nous fournissons une liste de « valeurs de sortie ». Toute valeur écrite dans une valeur de « sortie » sera « retournée » par la fonction. L'argument x est bien sûr l'argument d'entrée dans la fonction. La fonction retourne la valeur r, qui est le carré de x.

La question évidente est : qu'en est-il si nous souhaitons retourner deux valeurs ? Essayons ceci à l'invite de Scilab :

-->function [r1, r2] = foo (x, y)
-->  r1 = x + y
-->  r2 = x - y
-->endfunction
 
-->[p, q] = foo(10, 20)
 q  =
 
  - 10.  
 p  =
 
    30.  
 
-->

Notez la manière spéciale dont nous appelons la fonction. La valeur de r1 sera transférée vers p et la valeur de r2 vers q.

Les invocations suivantes de « foo » démontrent le fait que le langage est typé dynamiquement.

-->[p, q] = foo([1,2], 1)
 q  =
 
!   0.    1. !
 p  =
 
!   2.    3. !
 
-->[p, q] = foo([1,2], [3,4,5])
 !--error     8 
inconsistent addition
at line       2 of function foo   called by :  
[p, q] = foo([1,2], [3,4,5])
 
-->

Il est possible d'enregistrer des définitions de fonctions dans un fichier et de les charger ultérieurement. Supposons que la défnition de fonction ci-dessus soit enregistrée dans un fichier appelé fun.sci. Il nous suffit d'=invoquer, à l'invite de Scilab :

-->exec('fun.sci')

7. Fourier entre en scène !

Nous rencontrons des « signaux » partout. Le haut-parleur d'un PC génère du son en convertissant des signaux électriques en vibrations. Nous voyons des objets autour de nous parce que ces objets font rebondir des signaux lumineux vers nos yeux. Nos postes de télévision et de radio reçoivent des signaux électromagnétiques. Nous sommes immergés dans un « océan de signaux » ! L'analyse des signaux est donc d'une importance cruciale dans de nombreuses branches de la science et de l'ingénierie.

La philosophie fondamentale d'Unix est « Keep it simple, stupid » (littéralement, « Gardez-le simple, stupide »). Souvent, les physiciens (comme la plupart des autres scientifiques et ingénieurs) ne peuvent pas adhérer à ce précepte lorsqu'ils démarrent une analyse, simplement parce que les phénomènes qu'ils étudient sont d'une complexité impressionnante. Il semble néanmoins que la majorité des choses complexes de ce monde peuvent s'expliquer en se fondant sur d'autres, plus simples. La perception de Joseph Fourier était que des signaux variant de façon complexe dans le temps peuvent être exprimés sous la forme d'une combinaison de courbes sinus/cosinus simples de fréquence et d'amplitude variables. Nous vérifierons cette hypothèse en représentant graphiquement quelques équations simples avec l'aide de Scilab.

Commençons par une simple somme de deux signaux sin.

-->delta = (2*%pi)/240
 delta  =
 
    0.0261799  

-->x = 0:delta:2*%pi

-->a = sin(x) - (1/2)*sin(2*x)
-->plot(x, a)

Voici le graphique :

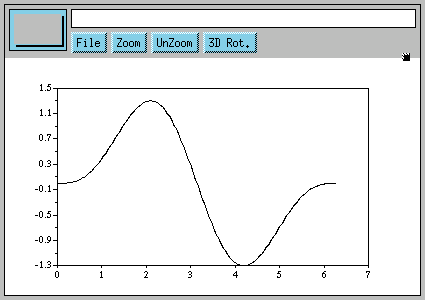
Il n'y a presque aucune indication ici que quelque chose d'intéressant va se produire. À présent, essayons une représentation graphique.

b = sin(x) - (1/2)*sin(2*x) + (1/3)*sin(3*x)

Continuons à ajouter des termes à la série : le prochain sera -(1/4)*sin(4*x), le suivant +(1/5)*sin(5*x), et ainsi de suite. Voici ce que j'ai obtenu en réalisant le graphique de cette série contenant 200 termes (vous devrez écrire une fonction pour ce faire) :

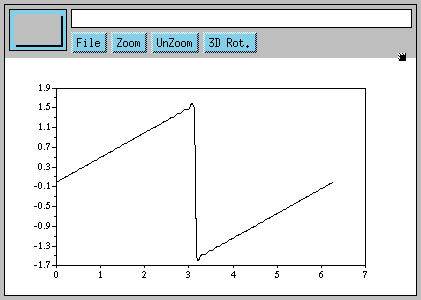
Tout cela semble magique ! La courbe sinus a complètement disparu, et nous avons un tout nouveau signal ! Comment Fourier « savait-il » qu'une telle série, qui nous donnerait finalement quelque chose de totalement différent de la somme de ses éléments, serait traitée de manière plus appropriée dans une classe mathématique ? Avons-nous un exemple d'enseignement des mathématiques plus « pratique », avec des étudiants ayant accès à des ordinateurs sous Linux exécutant Scilab, Python(Numeric), et une profusion d'autres outils libres et éducatifs ?)

8. Détermination des composants d'un signal

Nous avons vu qu'ajouter ensemble des sinus de fréquence et d'amplitude différentes nous donne des signaux qui semblent totalement différents. Maintenant, la question est : Supposons quelques nombres qui représentent une forme d'onde complexe, serons-nous en mesure d'indiquer quelle combinaison de sinus (fréquence et amplitude) a donné lieu à ce signal particulier ? Essayons.

Écrivons d'abord une fonction qui exécute une « intégration » numérique simple sur l'intervalle 0 à 2*PI. Divisons la surface située sous notre courbe en bandes minces, chacune d'une largeur de 2*PI/240, par exemple. La surface d'une bande au point x (0 < x < 2*PI) sera égale à sa hauteur multipliée par la largeur, ce qui donnera sin(x) * (2*PI/240). Ceci est l'idée à l'origine de la fonction d'intégration, qui peut être saisie à l'invite de Scilab. L'argument à intégrer est un vecteur des valeurs sinus dans l'intervalle 0 à 2*PI-delta, où delta est égal à (2*PI)/240. La différence entre deux valeurs successives dans le vecteur correspond à delta.

-->function [r] = integrate(a)
-->  r = sum(a)*(2*%pi)/240
-->endfunction

Essayons d'intégrer la fonction sinus simple, sin(x).

-->x = 0:delta:(2*%pi-delta)

-->integrate(sin(x))
 ans  =
 
    3.837E-16  

Nous constatons que l'intégrale est égale à zéro. La courbe sinus a une surface équivalente au-dessous et au-dessous du point zéro.

Essayons de représenter le graphique de sin(x).*(-sin(x)). (Notez que l'opérateur .* exécute la multiplication membre à membre de deux vecteurs) :

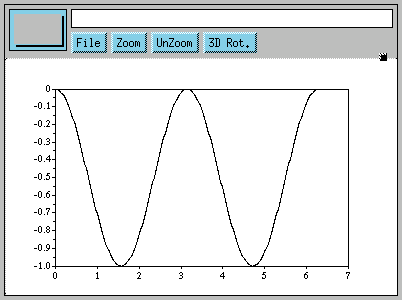
Nous constatons que la fonction a été complètement décalée au-dessous du point zéro. Elle devrait maintenant avoir une surface non nulle.

-->integrate(sin(x).*(-sin(x))) 
 ans  =
 
  - 3.1415927  
 
-->

Scilab indique qu'il s'agit de -PI. Essayons à présent de représenter graphiquement sin(2*x).*(-sin(x)) :

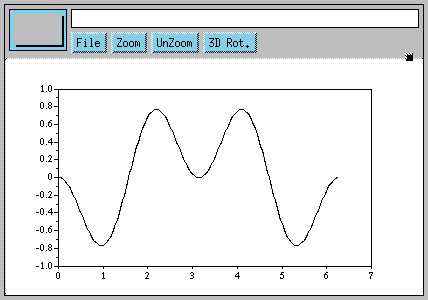
Le graphe indique que l'intégrale devrait être égale à zéro. Vérifions-le :

-->integrate(sin(2*x).*(-sin(x)))  
 ans  =
 
    3.977E-16  

Nous commençons à présent à avoir une « idée » de ce que nous emploierons pour séparer les composants de notre signal complexe. Multiplier un sinus par la négative d'un sinus d'une fréquence différente donne zéro — nous obtenons des résultats non nuls uniquement lorsque les fréquences correspondent. Supposons que notre signal complexe soit :

sin(x) - (1/2)*sin(2*x) + (1/3)*sin(3*x) - (1/5)*sin(5*x)

Multiplier ceci par -sin(x) permet d'obtenir :

sin(x).*(-sin(x)) - (1/2)*sin(2*x).*(-sin(x)) + 
(1/3)*sin(3*x).*(-sin(x)) - (1/5)*sin(5*x).*(-sin(x))

Le premier terme donne -PI, tous les autres termes deviennent nuls. Le fait d'obtenir une valeur non nulle nous indique que sin(x) est présente dans le signal. Maintenant, multiplions le signal par -sin(2*x) : si nous obtenons un résultat non nul, cela signifie que sin(2*x) est présente dans le signal. Nous répéterons ce processus autant de fois que nous le souhaitons.

Comment faire pour obtenir l'amplitude de chaque composant ? Faisons une autre expérience :

-->b = sin(x) - (1/2)*sin(2*x) + (1/3)*sin(3*x) - (1/4)*sin(4*x)
 
-->integrate(b.*(-sin(x)))                                      
 ans  =
 
  - 3.1415927  
 
-->integrate(b.*(-sin(2*x)))
 ans  =
 
    1.5707963  
 
-->integrate(b.*(-sin(3*x)))
 ans  =
 
  - 1.0471976  
 
-->integrate(b.*(-sin(4*x)))
 ans  =
 
    0.7853982  

Nous constatons qu'en divisant chaque résultat par -PI, nous obtenons l'amplitude de chaque composant du signal.

9. Conclusion

Il existe des outils propriétaires de très grande qualité pour faire du calcul numérique/symbolique — mais leur prix est parfois hors de portée de l'étudiant ou de l'amateur. J'espère que cet article vous a convaincu qu'il existe des alternatives dans le Logiciel Libre. Je vous saurais gré de m'informer de tout inexactitude que vous pourriez trouver dans ce document. Contactez-moi via ma page d'accueil sur http://pramode.net.

10. Remerciements

Merci à l'équipe Scilab d'avoir créé un si merveilleux outil et de le documenter d'une manière aussi approfondie. Cet article n'aurait pas pu écrit sans l'aide du document de Chris Meyers, qui décrit les mathématiques de Fourier. Chris a aussi écrit d'autres programmes Python très intéressants qui vous passionneront à coup sûr. Un grand merci à lui !

Je suis formateur et travaille pour IC Software® à Kerala (Inde). J'aurais aimé travailler dans le domaine de la chimie organique, mais je donne le meilleur de moi-même à ma seconde passion, jouer avec Linux et enseigner la programmation !