GNU Octave — Une introduction
Gazette Linux n°109 — Décembre 2004
Barry O'Donovan
Copyright © 2004 Barry O'Donovan
Copyright © 2004 Joëlle Cornavin
Copyright © 2004 François Poulain
Article paru dans le n°109 de la Gazette Linux de décembre 2004.
Traduction française par Joëlle Cornavin
<jcornavi CHEZ club TIRET internet POINT fr>.
Relecture de la traduction française par François Poulain
<fpoulain CHEZ enib POINT fr>.
Article publié sous Open Publication License. La Linux Gazette n'est ni produite, ni sponsorisée, ni avalisée par notre hébergeur principal, SSC, Inc.
- Table des matières
- 1. Installation et exécution d'Octave
- 2. Documentation
- 3. Premiers pas par l'exemple
- 4. Types de données, arithmétique simple et fonctions standard
- 5. L'environnement Octave
- 6. Boucles et instructions conditionnelles
- 7. Bref aperçu des fonctionnalités d'Octave
- 8. Conclusion
- 9. Le mois prochain
Voici le premier d'une série d'articles dans laquelle je présenterai GNU Octave et démontrerai quelques-unes de ses nombreuses fonctionnalités. GNU Octave est un langage haut niveau pour le calcul numérique. Je l'utilise au quotidien pour ma thèse de doctorat, ce qui implique de manipuler de grands vecteurs et matrices. Il est très similaire en termes de syntaxe et de fonctions à une application commerciale appelée Matlab. La principale différence entre les deux réside dans leur mode de publication. Octave est diffusé sous l'égide de la GNU General Public License, ce qui signifie qu'il peut être distribué et/ou modifié gratuite(libre)ment, alors qu'une licence étudiant mono-utilisateur pour le Matlab de base coûte actuellement 575 euros environ.
J'ai convaincu quelques-uns de mes collègues d'essayer Octave au lieu de Matlab. Dans tous les cas, dès lors qu'une personne arrête de chercher les différences entre les deux et qu'elle décide de donner à Octave une chance réelle, elle commence à saisir son utilité, ses fonctionnalités et sa disponibilité gratuite. Elle réalise qu'elle peut installer une copie d'Octave sur chacun de ses serveurs de simulation, de ses ordinateurs portables et domestiques, sans avoir à acheter de nouvelles licences coûteuses pour chacun.
1. Installation et exécution d'Octave
Vous pouvez télécharger le code source d'Octave sur son site, http://www.octave.org/download.html, qui contient aussi des informations sur l'endroit où obtenir Octave sous forme binaire pour les systèmes d'exploitation OS X d'Apple® et Windows. La plupart des distributions GNU/Linux offrent Octave en standard et, si ce n'est pas le cas sur votre système, il suffit d'installer le paquetage Octave à partir de vos cédéroms d'installation ou de l'Internet.
Démarrer l'interpréteur Octave sous GNU/Linux est aussi simple que saisir la commande octave :
$ octave GNU Octave, version 2.1.53 (i586-mandrake-linux-gnu). Copyright (C) 2004 John W. Eaton. This is free software; see the source code for copying conditions. There is ABSOLUTELY NO WARRANTY; not even for MERCHANTIBILITY or FITNESS FOR A PARTICULAR PURPOSE. For details, type `warranty'. Please contribute if you find this software useful. For more information, visit http://www.octave.org/help-wanted.html Report bugs to <bug-octave@bevo.che.wisc.edu> (but first, please read http://www.octave.org/bugs.html to learn how to write a helpful report). octave:1> |
2. Documentation
Un manuel de 380 pages est inclus dans le code source d'Octave aux formats HTML, DVI et PS. Ce manuel est également disponible en ligne sur la page d'accueil du projet Octave. Si vous avez procédé à l'installation au moyen des paquetages binaires, vous devriez pouvoir accéder au manuel à l'aide de la commande info :
$ info octave |
Si vous n'êtes pas à l'aise avec info, essayez l'interface de KDE à info en saisissant info:octave dans la barre d'URL de Konqueror.
Dans cet article, je n'aborderai que les notions essentielles d'Octave, simplement pour démontrer comme il est facile à acquérir et à utiliser efficacement. Je ne saurais trop recommander, au minimum, de parcourir la documentation disponible pour s'imprégner pleinement de ce qu'Octave a à offrir.
3. Premiers pas par l'exemple
Examinons le problème consistant à résoudre un système de n équations linéaires à n inconnues :
x + 3y - 2z = -3
3x - 4y + 3z = 28
5x - 5y + 4z = 7
|
Un tel système d'équations linéaires peut s'écrire comme une simple équation matricielle Ax = b, où A est la matrice coefficient, b le vecteur de colonne contenant le second membre des équations linéaires et x le vecteur de colonne représentant la solution. Si vous avez oublié votre algèbre linéaire, ne vous inquiétez pas — tout deviendra beaucoup plus clair au fur et à mesure que nous ferons appel à Octave pour résoudre ce système à notre place :
octave:1> A = [ 1, 3, -2; 3, -4, 3; 5, 5, -4 ]
A =
1 3 -2
3 -4 3
5 5 -4
octave:2> b = [ -3; 28; 7 ]
b =
-3
28
7
octave:3> A \ b
ans =
5.0000
2.0000
7.0000
octave:4>
|
Vous remarquerez que chaque ligne de l'interpréteur est numérotée séquentiellement ; j'utiliserai ces numéros de ligne lorsque je ferai référence à des commandes particulières. Sur la ligne 1, j'ai défini A comme une matrice 3x3 contenant les coefficients du système linéaire ci-dessus (un coefficient est le nombre placé à gauche des variables inconnues x, y et z). Les lignes sont délimitées par un point-virgule et les éléments individuels sur chaque ligne sont délimités par une virgule. Chacun d'entre eux est recommandé mais optionnel : un espace suffit pour délimiter des élements dans une ligne et on aurait pu utiliser la touche Entrée au lieu de points-virgules. J'ai défini le vecteur de colonne b sur la ligne 2 de la même manière.
La ligne 3 calcule la solution du système linéaire à l'aide de l'opérateur de « division à gauche » qui, pour les mathématiciens parmi vous, est d'un point de vue conceptuel équivalent à A-1b. Par solution, je veux dire que x = 5, y = 2 et z = 7 satisferont l'ensemble des trois équations du système linéaire.
Représenter graphiquement la solution d'un problème en mathématiques est souvent la clé pour comprendre pleinement ce problème. Octave comporte un certain nombre de fonctions pour tracer des graphes en deux et trois dimensions qui utilisent gnuplot pour manipuler les graphiques proprement dits. À titre d'exemple simple, traçons sin( x ) :
octave:9> x = [ -pi:0.01:pi ]; octave:10> plot( x, sin(x) ) octave:11> |
Ce qui donne :
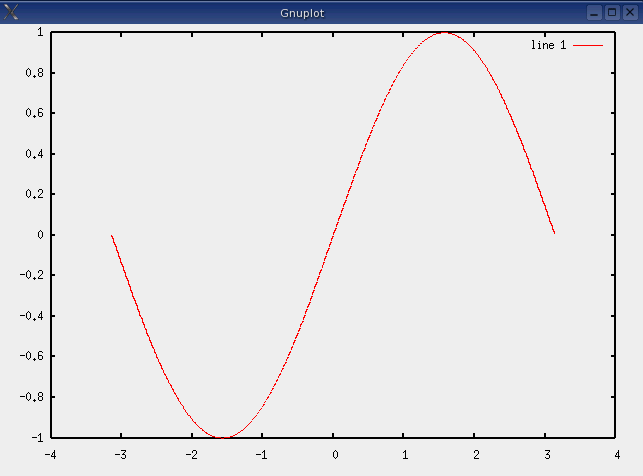
Observons la ligne 9 ci-dessus plus en détail :
piest une des nombreuses constantes intégrées à Octave pour plus de commodité et vaut 3,1415...Octave a un opérateur INTERVAL de la forme début:pas:fin, de telle sorte que [ 1:1:5 ] est le vecteur [ 1 2 3 4 5 ]. Le pas est optionnel et, s'il est omis, une taille de pas de 1 est supposée : 1:1:5 est identique à 1:5.
Vous avez peut-être remarqué que la ligne 9 ci-dessus n'a produit aucune sortie à l'écran, comme les commandes similaires l'ont fait auparavant. C'est parce que nous avons terminé la commande par un point-virgule, ce qui supprime la sortie. Dans le cas ci-dessus, [ -pi:0.01:pi ] crée un vecteur d'une longueur de 629, que nous ne tenons pas vraiment à afficher à l'écran !
4. Types de données, arithmétique simple et fonctions standard
Les types de données intégrés d'Octave sont des réels, des scalaires et des matrices complexes, des chaînes de caractères et un type de structure de données. La totalité des fonctions arithmétiques standard est disponible pour les scalaires et les matrices :
a + b (a - b) | Addition (soustraction). Si les deux opérandes sont des matrices, alors le nombre de lignes et de colonnes doit également correspondre. Si un seul opérande est un scalaire et l'autre une matrice, alors ce scalaire sera ajouté (soustrait) à (de) chaque élément de la matrice. |
a .+ b (a .- b) | Addition par composante (soustraction) (également dénommée « addition élément par élément »). |
| x * y | Multiplication. Si les deux opérandes sont des matrices, alors le nombre de colonnes de x doit s'accorder avec le nombre de lignes de y. |
| x .* y | Multiplication par composante. |
| x / y | Division à droite. Équivalent d'un point de vue conceptuel à ( (yT)-1* xT )T. |
| x ./ y | Division à droite par composante. |
| x \ y | Division à gauche. Équivalent d'un point de vue conceptuel à x-1 * y. |
| x .\ y | Division à gauche par composante. |
x ^ y x ** y | Opérateur de puissance. Reportez-vous au manuel pour les définitions, quand x et/ou y est une matrice. |
| x .** y | Opération sur les puissances par composante. |
| -x | Négation |
| x' | Transposition conjuguée complexe. |
| x.' | Transposition. |
Il y a de nombreuses fonctions standard intégrées à Octave, qui comprennent :
les fonctions scalaires
les fonctions vectorielles
les fonctions matricielles
eig()- valeurs propres et vecteurs propresinv()- inversepoly()- polynôme caractéristiquedet()- déterminantsize()- retourne la taille d'une matricenorm(,p)- calcule la norme -p d'une matricerank()function- le rang d'une matrice
Les chaînes peuvent être déclarées soit avec des apostrophes, soit avec des guillemets :
> fname = "Barry"; > sname = "O'Donovan"; |
Les chaînes peuvent être concaténées en utilisant la même notation que les définitions des matrices :
> [ fname, " ", sname ] ans = Barry O'Donovan |
Il y a de nombreuses fonctions de chaînes disponibles en standard, dont des fonctions pour convertir des chaînes en nombres et vice versa. On trouve aussi un certain nombre de fonctions servant à afficher des chaînes à l'écran, telles que disp() et printf(), ainsi que pour lire des données provenant de l'utilisateur, telles que input().
5. L'environnement Octave
Dans tous les cas ci-dessus où nous avions une commande d'affectation telle que A = ..., la variable A est créée ou écrasée par les informations situées du côté droit de l'opérateur d'affectation (=). Les noms de variables sont sensibles à la casse et sont composés de lettres, de chiffres et de caractères de soulignement mais doivent commencer par une lettre ou un caractère de soulignement. Les variables restent dans l'environnement de l'interpréteur jusqu'à ce que sortiez de l'interpréteur ou que vous effaciez la variable :
> clear A |
supprime la variable A, alors que :
> clear |
supprime toutes les variables actuellement stockées. La commande who peut servir à répertorier toutes les variables actuellement stockées dans l'environnement.
Nous serons souvent amenés à enregistrer l'environnement actuel sur disque sous forme de sauvegarde ou pour y revenir plus tard et poursuivre à partir de l'endroit nous nous sommes arrêtés. Nous pouvons utiliser les deux commandes suivantes pour ce faire :
> save nom_de_fichier |
pour enregistrer toutes les variables actuellement définies sous un nom de fichier et :
> load nom_de_fichier |
pour les charger à nouveau à un stade ultérieur.
6. Boucles et instructions conditionnelles
Comme n'importe quel autre langage de programmation, Octave a ses structures de contrôle (boucles et instructions conditionnelles). L'exemple suivant montre comment générer les dix premières valeurs de la séquence de Fibonacci à l'aide d'une boucle for :
octave:11> fib = [ 0, 1 ]; octave:12> for i = 3:10 > fib = [ fib, fib( i-2 ) + fib( i-1 ) ]; > endfor octave:13> fib fib = 0 1 1 2 3 5 8 13 21 34 octave:14> |
La séquence de Fibonacci est décrite par Fk = Fk-1 + Fk-2 avec F0 = 0 et F1 = 1. On l'utilise souvent pour décrire l'augmentation de population des lapins : supposez qu'un couple de lapins nouveaux-nés ne produise aucune progéniture durant le premier mois de leur vie et ne produise qu'un nouveau couple chaque mois suivant. En commençant par F1 = 1 couple(s) le premier mois, Fk est le nombre de couples durant le ke mois, en supposant qu'aucun des lapins ne meure. La séquence de Fibonacci se produit naturellement dans divers domaines et c'est une de ces rares occurrences en mathématiques où une formule simple peut être réellement fascinante.
Notez que dans le code ci-dessus :
nous redéfinissons le vecteur
fibà l'aide de lui-même et d'une nouvelle valeur ; etnous pouvons accéder aux éléments individuels d'un vecteur en spécifiant son numéro d'élément entre parenthèses.
L'exemple suivant évalue le caractère aléaotoire de la fonction rand() d'Octave et démontre ses instructions conditionnelles :
octave:14> a = b = c = d = 0; octave:15> for i = 1:100000 > r = rand(1); > if ( r < 0.25 ) > a++; > elseif ( r < 0.5 ) > b++; > elseif ( r < 0.75 ) > c++; > else > d++; > endif > endfor octave:16> a,b,c,d a = 25115 b = 24870 c = 25045 d = 24970 octave:17> |
La ligne 14 positionne les variables scalaires a, b, c et d à zéro. Nous générons alors 100 000 nombres aléatoires entre 0 et 1, puis nous augmentons a de 1 si elle tombe entre 0 et 0,25, b si elle tombe entre 0,25 et 0,5, et ainsi de suite. Une fois la boucle complète, nous nous attendrions à ce que les valeurs de a, b, c et d soient approximativement 25 000 si rand() génère des nombres véritablement aléatoires, ce qui, comme nous l'avons vu précédemment, est le cas.
7. Bref aperçu des fonctionnalités d'Octave
Octave a été écrit à l'origine et est toujours maintenu par John W. Eaton, qui en a réalisé la première version publique en 1993. Depuis, de nombreuses autres personnes y ont contribué car elles trouvaient qu'il manquait des fonctionnalités dont elles avaient besoin. Tel quel, Octave est fourni avec de nombreuses fonctions intégrées groupées en paquetages interdépendants.
La manipulation des matrices est au cœur d'Octave et comprend tous les opérateurs que vous attendez en matière d'arithmétique matricielle, dont l'addition, la soustraction, la multiplication (matricielle et par composante), la division, la transposition, etc. Elle offre aussi un certain nombre de fonctions pour générer des matrices courantes, dont :
eye() - la matrice d'identité
ones() et zeros() - une matrice pour tous les 1 ou les 0
hankel() - la célèbre matrice de Hankel et
hilb() et invhilb() - la matrice de Hilbert et la matrice de Hilbert() inverse
Les groupes de fonctions spécialisées comprennent des fonctions :
d'entrée et sortie
de représentation graphique
de manipulation des matrices
d'algèbre linéaire
d'équations non linéaires
d'équations différentielles
d'optimisation
statistiques
financières
d'ensembles
de manipulations de polynômes
de théorie de contrôle
de traitement du signal
de traitement d'images et
de traitement audio
Certains sont complets, alors que d'autres ne contiennent que quelques fonctions. Chacune est ajoutée par diverses personnes, en fonction des besoins. Ces deux prochains mois, nous verrons comment créer de nouvelles fonctions avec Octave et comment écrire de nouvelles fonctions en C++. Les développeurs d'Octave feront bon accueil aux nouveaux ajouts et si tout se passe bien d'ici à la fin de cette série, vous pourriez écrire et contribuer à vos propres fonctions Octave.
8. Conclusion
J'espère que cet article aura démontré combien il est facile d'acquérir les bases d'Octave. Pour les professeurs ou les maîtres de conférence qui tentent d'enseigner à leurs étudiants les matrices et/ou l'algèbre linéaire, pourquoi ne pas présenter Octave en cours comme outil d'enseignement ? Et pour les maîtres de conférence ou les étudiants de départements universitaires tels que les mathématiques, la physique mathématique, la physique, l'ingénierie, l'informatique, etc. — il est souvent difficile de devoir inventer des projets de fin d'année nouveaux et passionnants tous les ans. Pourquoi ne pas demander à un étudiant de mettre en œuvre un peu de fonctionnalité mathématique qui fait défaut à Octave à partir d'un secteur de recherche propre, qui pourrait être intéressant pour d'autres ?
9. Le mois prochain
L'écriture de nouvelles fonctions Octave et de scripts Octave qui peuvent être exécutés sur la ligne de commande.
Barry O'Donovan est diplômé de la National University of Ireland (Galway), avec un B.Sc. (Hons) en informatique et en mathématiques. Il prépare actuellement une thèse d'informatique avec le Information Hiding Laboratory, au University College Dublin (Irlande) dans le secteur du marquage numérique audio.
Barry utilise Linux depuis 1997 et son choix actuel va à Fedora Core. Il est membre du Irish Linux Users Group. Quand il ne travaille pas à sa thèse, on peut le voir faire un peu de Open Hosting, au pub avec ses amis ou faire de la course dans le parc de sa ville.